6 Introduzione alla grafica scientifica con R
v1.1 4/11/2023
6.1 Cosa c’è da imparare in questo capitolo.
In qualsiasi libro introduttivo su R il capitolo sulla grafica è probabilmente il più importante. I grafici (scientifici e non) sono sicuramente il modo più efficace di rappresentare i dati, viste le capacità degli esseri umani di percepire pattern in maniera prevalentemente visuale. R ha, senza dubbio, capacità di rappresentazione grafica dei dati (scientifici e non) molto superiori a quelle di altri ambienti e linguaggi per la data science. In aggiunta a questo, l’output grafico di R si presta bene ad essere inserito in documenti, app e dashboard interattive.
Puoi avere un’idea rapida di quello che può fare la grafica di base di R con il seguente comando:
>demo(graphics)Un’idea migliore può dartela questa bella gallery di grafici con R (preparati a sopportare un bel po’ di pubblicità).
Proprio per questo, è bene che tu dedichi un po’ di tempo a questo capitolo.
Nella sezione 6.2 cercherò di dara qualche informazione di base sui principi della rappresentazione grafica dei dati. Leggere questa sezione potrebbe risparmiarti molti mal di testa in futuro124.
Nella sezione 6.3 proverò a confrontare i diversi sistemi grafici disponibili in R: come sempre, con l’installazione base di R puoi fare molto (se non tutto) e molti pacchetti basano la loro grafica esclusivamente sulla grafica di base (6.9). D’altra parte, la grammatica della grafica, implementata da ggplot2, è sicuramente più semplice da imparare e si inserisce in maniera elegante nei flussi di lavoro tidy (ordinati). Per questa ragione, quasi tutto il capitolo sarà concentrato sulla grafica con ggplot2. Spenderò poi qualche parola sul salvataggio dei grafici in R, semplicissimo per la grafica generata da ggplot2, e appena un po’ più complicato (perché richiede il reindirizzamento dell’output dal display a un device o tipo di file, vedi sezione 6.4.1) con la grafica di base.
Infine, mi concentrerò sulla grafica (o meglio sulla visualizzazione di dati) con ggplot2, illustrando i principali tipi di grafici per variabili qualitative e/o quantitative (e tutte le loro possibili combinazioni).
Può sembrare strano, ma qualche cosina sulla grafica base R è necessario impararla (sezione 6.9): molti pacchetti importanti usano la grafica di base e personalizzare l’output richiede qualche conoscenza di questo sistema.
La capacità di produrre visualizzazioni dei dati efficaci, eleganti e convincenti è essenziale per qualsiasi scienziat* o analista dei dati. Per questo sarebbe bene leggere con attenzione tutto il capitolo. In alternativa, puoi dare una lettura veloce alla sezione 6.2, alla sezione 6.6 sui principi dell’uso di ggplot2, e concentrarti su quelli fra i paragrafi successivi che illustrano i tipi di grafico che sono più importanti per te. Potrai tornare sugli altri argomenti quando serve. Come sempre, i paragrafi di approfondimento hanno un titolo in corsivo.
6.2 I grafici, fatti bene.
La rappresentazione visuale dei dati è fondamentale il moltissimi campi e la cattiva rappresentazione dei dati è forse una delle basi principali delle diffidenza che molti nutrono per la statistica. L’ignoranza degli aspetti anche più elementari della visualizzazione dei dati da parte della stragrande maggioranza del pubblico è sicuramente un’altra ragione. Giornalisti (della carta stampata, del web e della televisione) ne fanno un largo (ab)uso e alcune infografiche sono talmente assurde da diventare dei veri e propri meme: questo articolo del blog Scienza in rete ne dà una rappresentazione, come dire, plastica. Non è detto, purtroppo, che gli scienziati facciano una lavoro migliore e, nella mia vita di ricercatore (e, purtroppo, di reviewer di articoli scientifici) ho visto cose che voi umani…
Produrre delle buone visualizzazioni di dati (che forse è un modo migliore di dire rispetto a grafici scientifici, che sembra troppo limitato alle pubblicazioni scientifiche) è una cosa che si impara (purtroppo non nell’università della strada), e si impara studiando. Nella sezione 6.10 troverai qualche suggerimento125. A questo dovremmo forse aggiungere il fatto che, come scienziati abbiamo forse qualche responsabilità in più: i grafici che generiamo dovrebbero rappresentare la realtà nella maniera più fedele e oggettiva possibile, e al tempo stesso, rispondere alle esigenze di informare, motivare e convincere, che sono proprie di qualsiasi forma di comunicazione. Se poi riusciamo anche a produrre grafici belli da vedere126 è meglio, mi pare.
Una trattazione estesa della tecnica e dell’arte della visualizzazione (scientifica) dei dati è decisamente al di là dello scopo di questo “libro”. Alcune cose però vanno dette.
Innanzitutto, è impossibile astrarre completamente dai pregi e dai difetti del nostro sistema di percezione. Gli esseri umani processano buona parte dell’informazione che raggiunge i sensi attraverso la vista e, tipicamente, perché questa informazione “resti” nella nostra memoria sono necessari diversi passaggi127: lo stimolo visivo viene inizialmente processato dalla memoria iconica, per poi passare nella memoria a breve (che include la memoria di lavoro visiva) e infine in quella a lungo termine. Mentre i primi passaggi sono largamente inconsci, il passaggio nella memoria a lungo termine richiede un processo di creazione di relazioni con quella che è la nostra conoscenza del mondo. Stimoli visivi poco contrastati o poco intensi potrebbero essere difficili da processare e la memoria a breve termine sembra essere in qualche modo limitata: il numero di elementi diversi che possono essere conservati prima del passaggio alla memoria a lungo termine è compreso fra 4 e 9.128.
Insomma, ritenere le informazioni che giungono al nostro sistema visivo richiede “lavoro” e ci sono dei limiti a quello che il nostro sistema di percezione può fare in un tempo limitato. Mentre se state leggendo un libro o un articolo scientifico potete dedicare quanto tempo volete ad un singolo grafico (o a una foto), se state guardando un video o una presentazione avete generalmente un tempo limitato. Pensate al fastidio che provate quando, dal fondo di un’aula o di una sala congressi affollata, guardate ad una presentazione con grafici troppo complessi, sfocati, poco contrastati o troppo ricchi di informazione, che magari restano sullo schermo 30 secondi. Difficilmente riuscirete a seguire ciò che chi parla vuole comunicare e entrambi avrete perso il vostro tempo.
Inoltre, lo scopo della visualizzazione scientifica dei dati è fornire informazioni in modo corretto e questo, tipicamente, richiede dei confronti quantitativi. La gerarchia (da migliore a peggiore) della nostra capacità di fare confronti fra valori è129:
posizione su una scala comune (per esempio quando si guarda alla posizione di diversi punti in un dot plot o linee in un rug plot, ma anche, per estensione, di punti in un grafico cartesiano)
posizione su scale non comuni (per esempio quando si confronta la posizione di punti su due grafici con assi cartesiani diversi presenti nella stessa figura)
lunghezza (quando per esempio si vuole confrontare la lunghezza dei box fra diversi box and whisker plot)
angoli o pendenze (per esempio in un grafico a coordinate angolari)
aree (per esempio quando si vuole confrontare la dimensione di punti in un bubble plot) e intensità di colore (usata per esempio per mappare una variabile quantitativa al colore di un punto)
colori diversi (usati, male, in moltissime situazioni e spesso senza tener presente il fatto che molti non hanno una percezione corretta dei colori)
E’ abbastanza ovvio che dovremmo attribuire le variabili più importanti alle posizioni gerarchiche più alte di questa scala. In molti grafici più complessi è necessario far percepire con chiarezza delle relazioni non quantitative, come relazioni di similarità (in un icon plot), inclusione (per esempio in una ellissi bivariata di densità), prossimità (in uno dei tantissimi grafici multivariati che servono a percepire la presenza di cluster nei dati), presenza di connessioni (per esempio in un dendrogramma o in un albero di decisioni o in un network), appartenenza allo stesso gruppo, etc.
Se non conosci i tipi di grafici che ho nominato nel paragrafo precedente, non preoccuparti, li incontrerai presto.
Progettare bene una visualizzazione scientifica non è quindi una cosa per niente banale: molto spesso ci si lascia guidare dall’istinto o dalle consuetudini di un determinato campo (nel mio, che mi occupo di ecologia microbica, sono abbastranza frequenti le visualizzazioni monstre, che richiederebbero parecchi minuti per cominciare, forse, a capirle, e che vengono mostrate per pochi secondi durante una presentazione).
Se ti interessa approfondire questi argomenti dai (uno o più di) uno sguardo ai molti bei libri che richiamo nella sezione 6.10. Fortunatamente, i default della grafica di base e di ggplot2 in R sono “intelligenti” e ti impediranno (a meno che tu non ti impegni veramente tanto) di fare molte sciocchezze che sono invece frequentissime nei grafici generati con Microsoft Excel e molti altri fogli di calcolo.
6.3 I sistemi grafici in R.
R ha tre sistemi grafici principali:
base: è il sistema di default, e viene installato insieme a R con i pacchetti graphics e grDevices; ha un numero limitato di comandi per generare grafici (barplot, boxplot, hist, pairs, plot, etc.) e una serie di comandi complementari per personalizzare il grafico aggiungendo punti, modificando assi, legende, etc. I grafici sono inviati a “devices”, come lo schermo (il device di default)130 o file.
lattice: richiede l’istallazione del pacchetto corrispondente131; il grafico viene creato da un unico comando (con un gran numero di parametri) e inviato a un device o a un file; è un sistema particolarmente adatto a grafici multivariati e alla creazione di sub-plot per gruppi di dati sulla base di variabili qualitative o quantitative (trellis plots).
ggplot2: richiede l’istallazione del pacchetto corrispondente (o del
tidyverse); i grafici vengono creati in “strati”, secondo il concetto della grammatica della grafica; una volta creato, il grafico, se assegnato ad un nome, può essere modificato con l’aggiunta di nuovi “strati” e salvato in una varietà di formati con un comando specifico (ggsave)
Un confronto per un grafico a dispersione fra i tre sistemi, con la configurazione e personalizzazione minima, è mostrato dalle tre figure successive per il data set mpg, che è a sua volta incluso in ggplot2.
La Figura 6.1 mostra la relazione fra il consumo (hwy, in galloni per miglio) di carburante in autostrada e la cilindrata (displ, in litri) ottenuta con il comando generico plot() della grafica di base.
# se necessario carica la library tidyverse dopo aver rimosso il segno # di commento
# library(tidyverse)
data(mpg)
plot(x = mpg$displ, y = mpg$hwy)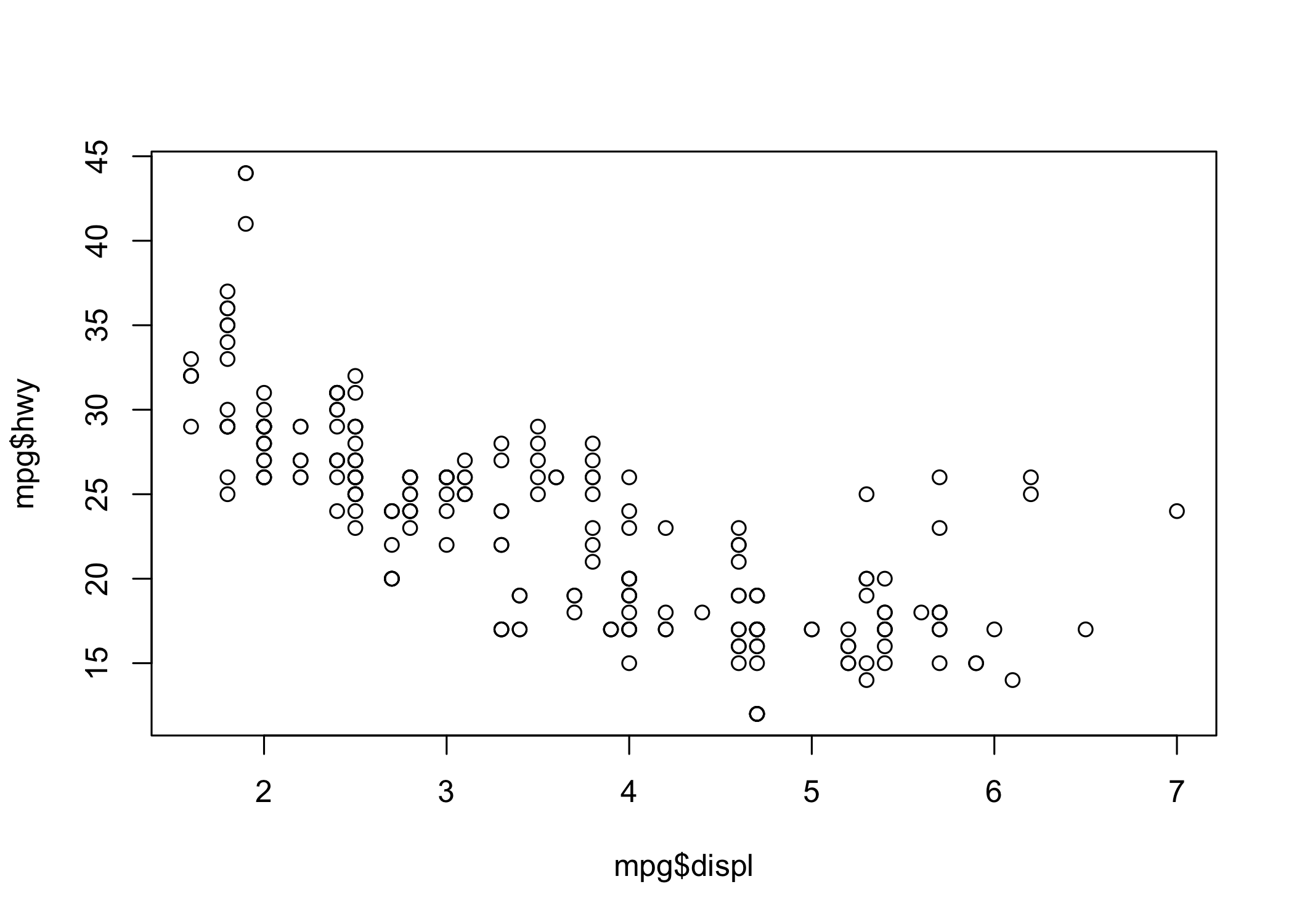
Figura 6.1: Un grafico a dispersione ottenuto con la grafica di base di R.
Qui vengono specificamente assegnati alle coordinate x e y due vettori, appartenenti allo stesso data set (in teoria possono essere 2 vettori numerici separati o addirittura due vettori in due data set diversi, ma della stessa lunghezza). Scale, etichette degli assi, simboli, titoli e sottotitoli, legende possono essere largamente personalizzati.
Le funzioni della grafica di base permettono di creare rapidamente (con il minimo di comandi) molti grafici semplici, che possono essere ulteriormente personalizzati. Inoltre, gli oggetti prodotti da molte funzioni della statistica di base o aggiunte con i pacchetti possono essere direttamente utilizzati nella funzione generica plot() generando grafici dipendenti dal contesto. Personalmente, trovo la sintassi della grafica di base difficile da ricordare. In aggiunta a questo, la creazione del grafico può essere piuttosto verbosa (cioé richiede molti comandi) perché i grafici vengono creati aggiungendo ad un oggetto creato da un comando di base (per esempio plot()) una serie di altre cose create da altri comandi (points(), legend(), lines()).
La Figura 6.2 mostra un trellis plot ottenuto con il comando xyplot di lattice. Qui la variabile qualitativa class è usata come variabile di gruppo. Fare la stessa cosa con la grafica di base è decisamente più complicato. Nota come in questo caso sto usando un’interfaccia formula, data, utilizzabile anche con plot. Le variabili dipendente e indipendente sono separate da una tilde ~ e la variabile di gruppo (quella che separa le singole osservazioni nei pannelli) è separata da una barra verticale | e il set di dati è indicato come data = mpg.
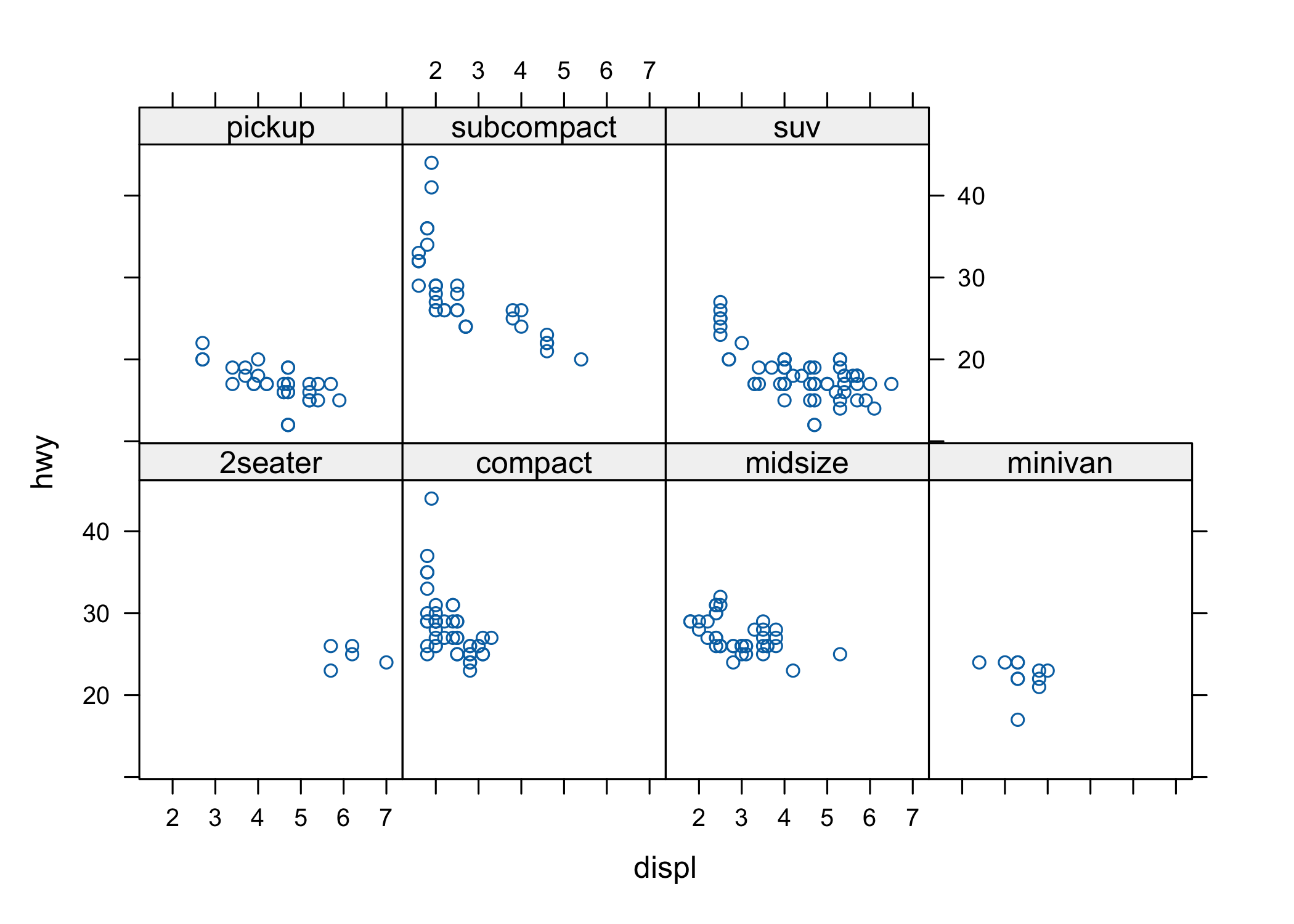
Figura 6.2: Un grafico a dispersione ottenuto con lattice.
Anche lattice è usato in molti pacchetti importanti (come per esempio car).
Come gli altri pacchetti del tidyverse, ggplot2 è molto più intuitivo, anche se i comandi possono essere più “verbosi”. Le già ragguardevoli capacità di ggplot2 sono estese da un gran numero di pacchetti aggiuntivi.
Infine, la figura 6.3 mostra l’equivalente della figura 6.2 ottenuto con ggplot2 (qui i pannelli sono generati dal comando facet_wrap()).
# library(ggplot2)
ggplot(data = mpg, mapping = aes(x = displ, y = hwy)) +
geom_point() +
facet_wrap(~class) 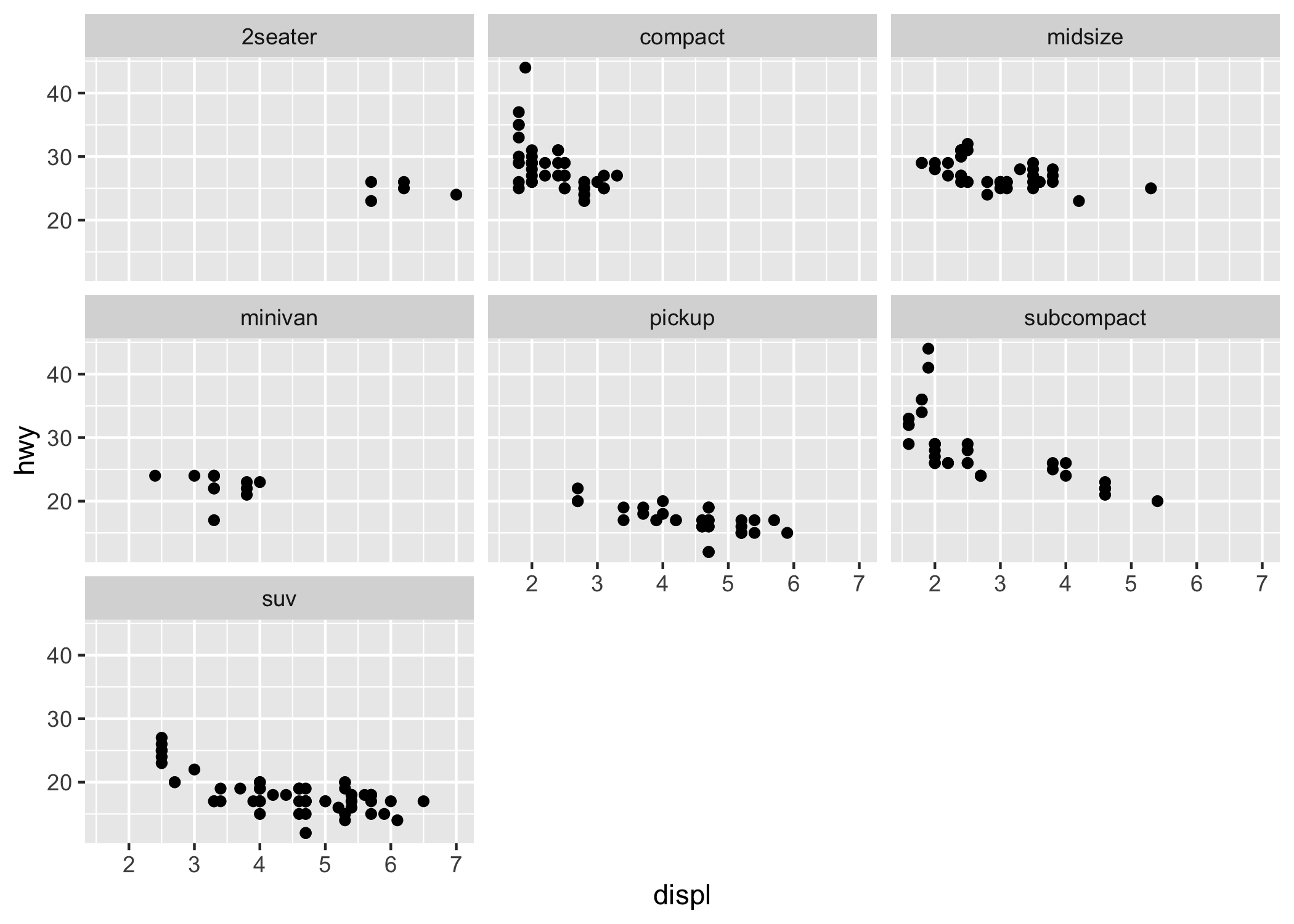
Figura 6.3: Un grafico a dispersione ottenuto con ggplot2.
Infine, quando diventerai più espert*, dovresti provare a esplorare i sistemi grafici interattivi, come ggvis e plotly.
6.4 Visualizzare o salvare i grafici: i device.
In R i grafici vengono inviati a quelli che si chiamano device. Di default, il device è lo schermo e il comando che viene usato dietro le quinte è specifico per piattaforma.
Prova a copiare e incollare in un nuovo script i seguenti comandi:
library(tidyverse) # potrebbe non essere necessario, se hai già caricato tidyverse
plot(x = mpg$displ, y = mpg$hwy)In RStudio, di default, i grafici prodotti da qualsiasi tipo di grafica vengono inviati al tab Plots del pannello Plot, ed è proprio in questo tab che dovresti vedere apparire il grafico. Se tu eseguissi lo stesso tipo di comando nella GUI di R, il grafico verrebbe inviato a una finestra che può aprirsi in un ambiente diverso (X11 su Mac)132.
Il Plots tab di RStudio offre diverse funzionalità utili (vedi capitolo 2), ma può causare alcuni problemi, legati al fatto che i grafici vengono ridimensionati in maniera dinamica (mentre magari potrebbe interessarti vedere il grafico così come potrebbe apparire se lo salvassi, vedi dopo, e lo aprissi in un’altra applicazione)133.
Il risultato dei comandi precedenti è questo:
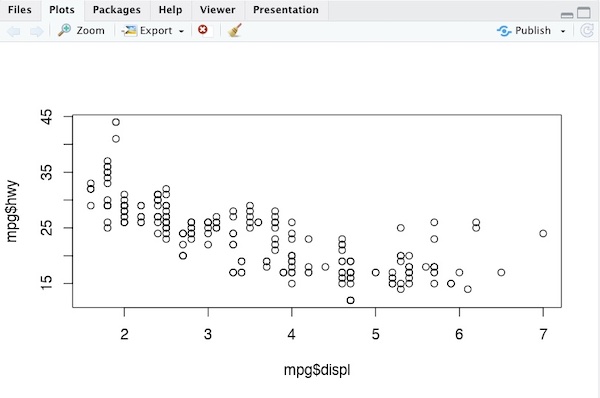
Figura 6.4: L’interfaccia di RStudio per MacOS.
Prova a fare quanto segue:
ridimensiona il tab “Plots” posizionando il puntatore sulla barra orizzontale o su quella verticale che delimitano il pannello: dovrebbe apparire una doppia frecccia, clicca con il mouse e ridimensiona il grafico;
clicca sul pulsante per lo
Zoomnella barra dei menu del tabPlots(quello con la lente di ingradimento): si apre una nuova finestra che puoi ridimensionare liberamente;clicca sul pulsante
Exportnella barra dei menu del tabPlots(quello con l’icona della piccola immagine); clicca su una delle opzioni, per esempio quellaSave as imagee scegli una delle opzioni. Se crei un’immagine bitmap (.tif, .jpg, .png, vedi dopo), e la apri con una app per la visualizzazione o modifica delle immagini, vedrai che la risoluzione è quella dello schermo (nel mio caso 96 dpi), che è ampiamente insufficiente per molte applicazioni.
6.4.1 Salvare i grafici: i file come device grafici.
Come hai appena visto, la risoluzione dei grafici creati nel plot pane è insufficiente per molte applicazioni: per un lavoro scientifico, tipicamente, è necessario sottomettere i grafici in formato vettoriale (.eps o .pdf) o sotto forma di immagini bitmap ad alta risoluzione (300 o 600 dpi). Per farlo, occorre salvare i grafici nel formato opportuno. La tabella 6.1 riporta un elenco dei device per i formati più frequentemente usati nella grafica scientifica, con qualche nota importante sulle proprietà di ciascun formato134.
| Device | Formato | Estensione | Tipologia | Antialias | Commenti |
|---|---|---|---|---|---|
| png | Portable Network Graphics | .png | bitmap | sì | adatto a siti web, supporta trasparenze |
| jpeg | Joint Photographic Experts Group | .jpeg, .jpg | bitmap | sì | permette una compressione (lossy) |
| bmp | Bitmap | .bmp | bitmap | sì | |
| tiff | Tagged Image Format | .tif, .tiff | bitmap | sì | consente diversi tipi di compressione |
| Portable Document Format | vettoriale | no | flessibile, leggibile su tutti i device | ||
| svg | Scalable Vector Graphics | .svg | vettoriale | sì | addatto all’uso online |
I formati vettoriali producono immagini che, in teoria, possono essere ingrandite a piacere, senza perdita di risoluzione e senza determinare una “scalettatura” delle linee. I formati bitmap registrano le immagini come un insieme di punti: per questa ragione la dimensione e la risoluzione sono essenziali nel determinare la massima dimensione alla quale un’immagine può essere riprodotta a video o in stampa senza perdite significative di qualità. Ingrandire un’immagine bitmap a bassa risoluzione o di piccole dimensioni (in cm o pollici/ inches, pixel) risulta in significative perdite di qualità: i singoli pixel diventano chiaramente visibili e le linee possono apparire come scalettate. La scalettatura può essere in parte attenuata dall’antialiasing. Naturalmente il prezzo dell’aumento della risoluzione o della dimensione fisica è l’aumento della dimensione del file. Quest’ultima può essere in parte controllata con la compressione (per i formati che la consentono): la compressione determina una perdita di qualità generalmente irreversibile, specialmente per le compressioni “lossy” usate per esempio dal formato .jpeg.
E allora, quale formato è meglio utilizzare?
ogni volta che è possibile è meglio usare i formati vettoriali (
.pdfper le applicazioni generali,.svgper le applicazioni su web). Tuttavia, non tutte le riviste scientifiche accettano grafici in formato.pdfe la resa di questo formato non è necessariamente uguale su tutti i sistemiper le altre applicazioni è meglio usare un formato bitmap, con una risoluzione sufficiente allo scopo:
.pngè un formato particolarmente adatto alle pagine web, che produce file di piccole dimensioni.bmpè un formato ingombrante ma piuttosto fedele.jpegè sicuramente il formato preferibile per immagini leggere, specialmente se con gradienti di colore, ma ha una compressione lossy.tiffun formato molto fedele ma ingombrante, che però permette una compressione; non tutte le codicieh di questo formato funzionano su tutti i sistemi operativi.
In generale, le riviste scientifiche richiedono una risoluzione di almeno 300 dpi (dot per inches) di dimensioni tali da occupare una o due colonne della “pagina” (ormai sempre più spesso virtuale, visto che quasi tutte le riviste sono on line). Per alcune applicazioni, e specialmente quando si usano gradienti di colore, potrebbe essere necessario usare una risoluzione di 600 dpi. I file prodotti dal formato preferito dalle riviste (.tif) possono essere veramente enormi (>10 Mb). Per applicazioni che richiedono una visualizzazione su schermo o su pagina e per le quali non si prevede che l’utente debba ingrandire l’immagine una risoluzione di 150-220 dpi può essere sufficiente. La risoluzione dello schermo (tipicamente 72 o 96 dpi) è sufficiente solo per una visualizzazione grafica delle immagini.
La figura 6.5, realizzata con ggplot2 con il dataset mpg può essere utilizzata come esempio per valutare l’effetto del tipo di formato o della compressione.
mpg %>% dplyr::filter(class %in% c("compact", "suv", "midsize", "subcompact")) %>%
ggplot(mapping = aes(x = cty, y = hwy)) +
geom_smooth(se = F) +
geom_point(mapping = aes(shape = class, color = displ), size = I(2)) +
labs(title = "Consumo di carburante per 32 modelli di auto",
subtitle = "anni 1999 - 2008",
x = "miglia per gallone in città",
y = "miglia per gallone in autostrada",
shape = "categoria",
color = "cilindrata, L",
caption = "Fonte: EPA, https://fueleconomy.gov/"
) +
scale_shape_manual(values = c(16,17,15,18)) +
scale_colour_continuous(type = "viridis") +
theme_bw() +
theme(plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5))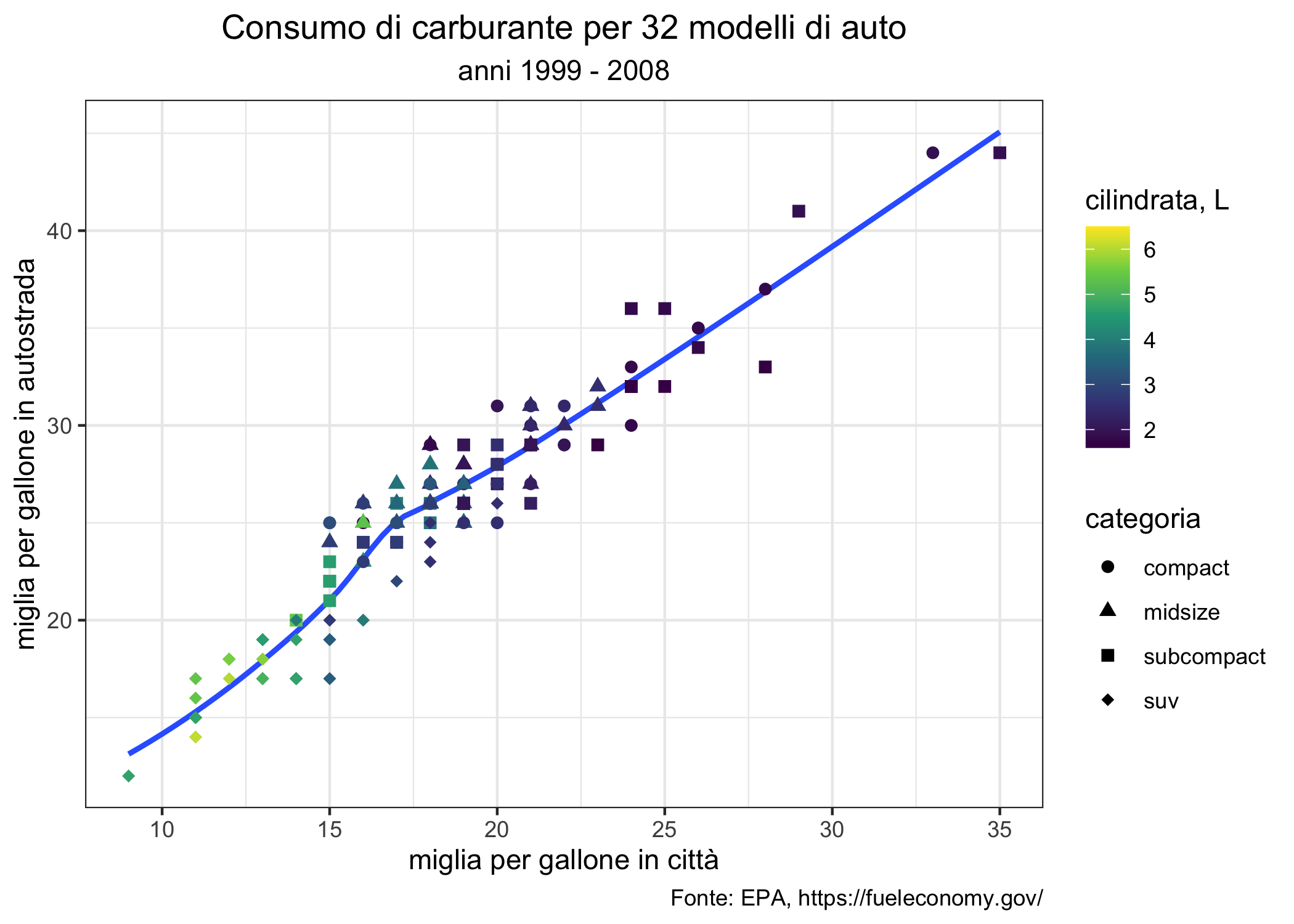
Figura 6.5: Un grafico a dispersione, con annotazioni, realizzato con ggplot2.
Nota come I(2) serva a assegnare uno degli elementi estetici ad un valore fisso (in questo caso la dimensione del simbolo) piuttosto che ad una delle variabili.
Ora prova a copiare e incollare il seguente codice in un nuovo script e ad eseguirlo. Come risultato:
prima creiamo il grafico e lo assegniamo ad un oggetto
poi mandiamo il grafico al device corrente
poi lo mandiamo ad un file .pdf (nella working directory), usando le opzioni di default
# qual'è il device attivo?
dev.cur()
# creiamo il plot e assegnamolo ad un oggetto
mpg_plot <- mpg %>% dplyr::filter(class %in% c("compact", "suv", "midsize", "subcompact")) %>%
ggplot(mapping = aes(x = cty, y = hwy)) +
geom_smooth(se = F) +
geom_point(mapping = aes(shape = class, color = displ), size = I(2)) +
labs(title = "Consumo di carburante per 32 modelli di auto",
subtitle = "anni 1999 - 2008",
x = "miglia per gallone in città",
y = "miglia per gallone in autostrada",
shape = "categoria",
color = "cilindrata, L",
caption = "Fonte: EPA, https://fueleconomy.gov/"
) +
scale_shape_manual(values = c(16,17,15,18)) +
scale_colour_continuous(type = "viridis") +
theme_bw() +
theme(plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5))
# inviamo il plot al device di default, il plot pane
mpg_plot
# ora inviamo ad un device pdf, con le opzioni di default
?pdf
# ATTENZIONE IL FILE PDF VIENE SALVATO CORRETTAMENTE SOLO SE VENGONO ESEGUITI
# ENTRAMBI I COMANDI SUCCESSIVI
pdf(file = "mpg_plot.pdf")
mpg_plot
# chiudiamo il device e restituisce l'output al device di default (il plot pane)
dev.off()
# ora apriamo un device png con le opzioni di default e una risoluzione di 72 dpi
?png
png(file = "mpg_plot.png", width = 7, height = 5, res = 72, units = "in")
# la lista dei device si ottiene con dev.list()
cat("the list of devices","\n", dev.list())
dev_list <- dev.list() # è un vettore con nomi
dev_list
# salviamo il grafico come .png, 72 dpi, 7x5 pollici
mpg_plot
# chiudiamo il device (non è necessario)
dev.off()
# ora .jpeg a due diverse risoluzioni, stessa dimensione, con la compressione
# di default (quality = 75)
jpeg(file = "mpg_plot_150.jpg", res = 150, width = 7, height = 5, units = "in")
mpg_plot
dev.off()
jpeg(file = "mpg_plot_300.jpg", res = 300, width = 7, height = 5, units = "in")
mpg_plot
dev.off()
# ora .tiff, non compresso, stessa dimensione
tiff(file = "mpg_plot_300.tiff", res = 300, width = 7, height = 5, units = "in")
mpg_plot
dev.off()Prova a verificare la dimensione dei diversi file, ad aprirli con la tua applicazione di default per la grafica e a zoommare: cosa succede ai colori? ai punti? alle linee?
6.4.2 Salvare i grafici di ggplot2 con ggsave.
I device funzionano con tutti i sistemi grafici, compreso ggplot2, che però mette a disposizione un sistema molto più semplice per salvare i grafici, il comando ggsave().
Prova ad eseguire questi comandi in uno script o nella console (è necessario aver creato l’oggetto grafico mpg_plot).
# l'aiuto su ggsave
?ggsave
ggsave(mpg_plot, filename = "mpg_plot_150.tiff", dpi = 150)ggsave() usa defualt intelligenti: determina il device dall’estensione del file e, se non si indica alcun oggetto da salvare, salva l’ultimo disponibile.
6.4.3 Le dimensioni del device e le opzioni grafiche.
Il device deve avere spazio sufficiente ad “accogliere” il grafico e tutti i suoi elementi (titoli, titoli degli assi, legende). Mentre il plot pane di RStudio viene ridimensionato dinamicamente e può essere ingrandito a piacere dall’utente, lo stesso non vale per i device bitmap. Prova a vedere cosa succede con questi comandi:
jpeg(file = "mpg_plot_150_480.jpg", res = 150)
mpg_plot
dev.off()A causa della maggiore risoluzione gli elementi del grafico non “entrano” nello spazio disponibile (480x480 pixel).
Un altro aspetto interessante è la personalizzazione delle diverse aree del device usando i parametri grafici.
Una trattazione estesa di questo argomento va decisamente al di là degli obiettivi di pigR135. In breve:
la dimensione del device può essere verificata usando
dev.size()136il device è diviso in due aree principali:
i margini, che ospitano gli assi e le loro etichette e i titoli e possono essere fissati, in pollici con il comando
par(mai = c(0.1,0.1,0.1,0.1)); i 4 numeri sono, in senso orario i margini inferiore, sinistro, superiore e destro;marpermette di fissare i margini in linee (lo spazio che ospita una linea o una colonna di testo)l’area del grafico, che può essere fissata, fra le altre cose fissando la dimensione per la larghezza e altezza in pollici:
par(pin = c(6.5,4.5))dà un’area grafica di 6,5 x 4,5 pollici
In realtà, è possibile operare in maniera molto più fine e persino dividere il device in aree (anche di divese dimensioni). La figura 6.6 fornisce un esempio di come il device possa essere diviso in due (1 riga, due colonne) per ospitare due grafici diversi.
# salva i parametri grafici correnti per poterli resettare facilmente
opar <- par(no.readonly = T)
# dividi il device in una riga con due colonne e riempi per righe
# (prima la prima colonna e poi la seconda)
par(mfrow = c(1,2))
# un grafico a dispersione
plot(hwy ~ cty, data = mpg)
# un grafico a barre
barplot(xtabs(~ class, data = mpg), las = 2)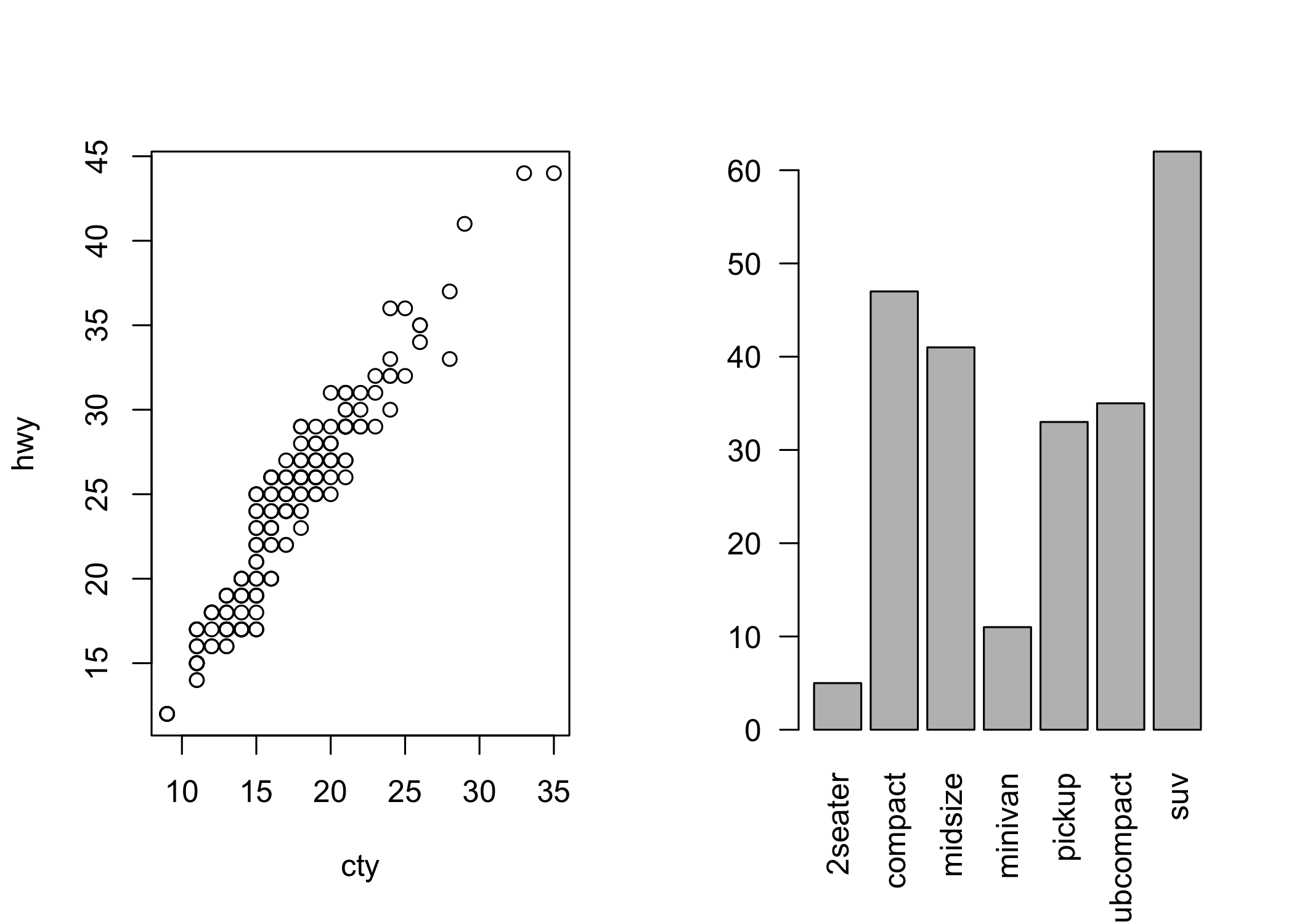
Figura 6.6: Dividere i devices.
Questo sistema permette una grande flessibilità nella divisione dell’area grafica ma richiede una buona conoscenza di tutti i parametri grafici. Ovviamente, come vedremo dopo, in R c’è sempre un sistema più semplice: il pacchetto cowplot, per esempio, permette di combinare gli oggetti grafici prodotti con ggplot2 con grande semplicità.
6.5 R, a colori.
L’uso del colore è critico per ottenere buone visualizzazioni di dati (leggi la sezione 6.2 per qualche dettaglio in più) ed R fornisce, tramite il pacchetto grDevices e molti pacchetti aggiuntivi, moltissimi strumenti per gestire al meglio i colori.
I colori possono essere utilizzati per:
distinguere diverse categorie: in questo caso sono adatti a variabili qualitative e i colori della palette usati in un grafico dovrebbero essere ottimizzati per distinguere al meglio le diverse categorie (che, idealmente, dovrebbero essere non più di 12, meglio se meno di 7);
rappresentare valori quantitativi; in questo caso si possono usare due tipi di scale cromatiche, con colori che formano un gradiente:
sequenziali: adatti a valori uniformemente crescenti o decrescenti;
divergenti: adatti a valori che divergono a partire da un valore centrale, tipicamente lo 0, come per esempio i valori di diversi indici di correlazione (che variano fra -1 e + 1)
In R i colori possono essere indicati con i loro nomi o mediante codici esadecimali che rappresentano i tre valori della scala RGB (rosso, verde, blu, ciascuno dei quali può variare da 0, assente, a 255, massima intensità). Una ottima cheatsheet sull’uso dei colori in R è disponibile qui.
Per visualizzare i nomi dei colori prova questi comandi nella console:
# i primi 20 e gli ultimi 20 colori (cambia il codice per visualizzare un
# elenco diverso dei 657 colori disponibili)
colors()[c((1:20), (length(colors())-20):length(colors()))]
# ottieni i nomi dei colori della palette in uso
# (quella di default all'avvio di R, può essere cambiata)
palette()
?palette
# per saperne di più sulle palette di grDevices
?rainbowLa Figura 6.7 mostra 6 palette sotto forma di diagrammi a torta.
opar <- par(no.readonly = T)
par(mfrow=c(2,3))
# la palette di default
pie(rep(1, length(palette())), col = palette(), labels = palette(),
main = "la palette di default")
# una palette arcobaleno a 6 colori
palette(rainbow(6))
lamiapalette <- palette()
pie(rep(1, length(lamiapalette)), col = palette(), labels = lamiapalette,
main = "una palette arcobaleno")
# una palette di 20 colori a gradiente di calore
palette(heat.colors(20))
lamiapalette <- palette()
pie(rep(1, length(lamiapalette)), col = palette(), labels = lamiapalette,
main = "una palette a gradiente di calore")
# una palette toporgrafica di 20 colori
palette(topo.colors(20))
lamiapalette <- palette()
pie(rep(1, length(lamiapalette)), col = palette(), labels = lamiapalette,
main = "una palette topografica")
# colori adatti per mappe
palette(terrain.colors(20))
lamiapalette <- palette()
pie(rep(1, length(lamiapalette)), col = palette(), labels = lamiapalette,
main = "una palette 'terreno'")
# una palette ciano-magenta, adatta a daltonici
palette(cm.colors(20))
lamiapalette <- palette()
pie(rep(1, length(lamiapalette)), col = palette(), labels = lamiapalette,
main = "una palette cyano-magenta")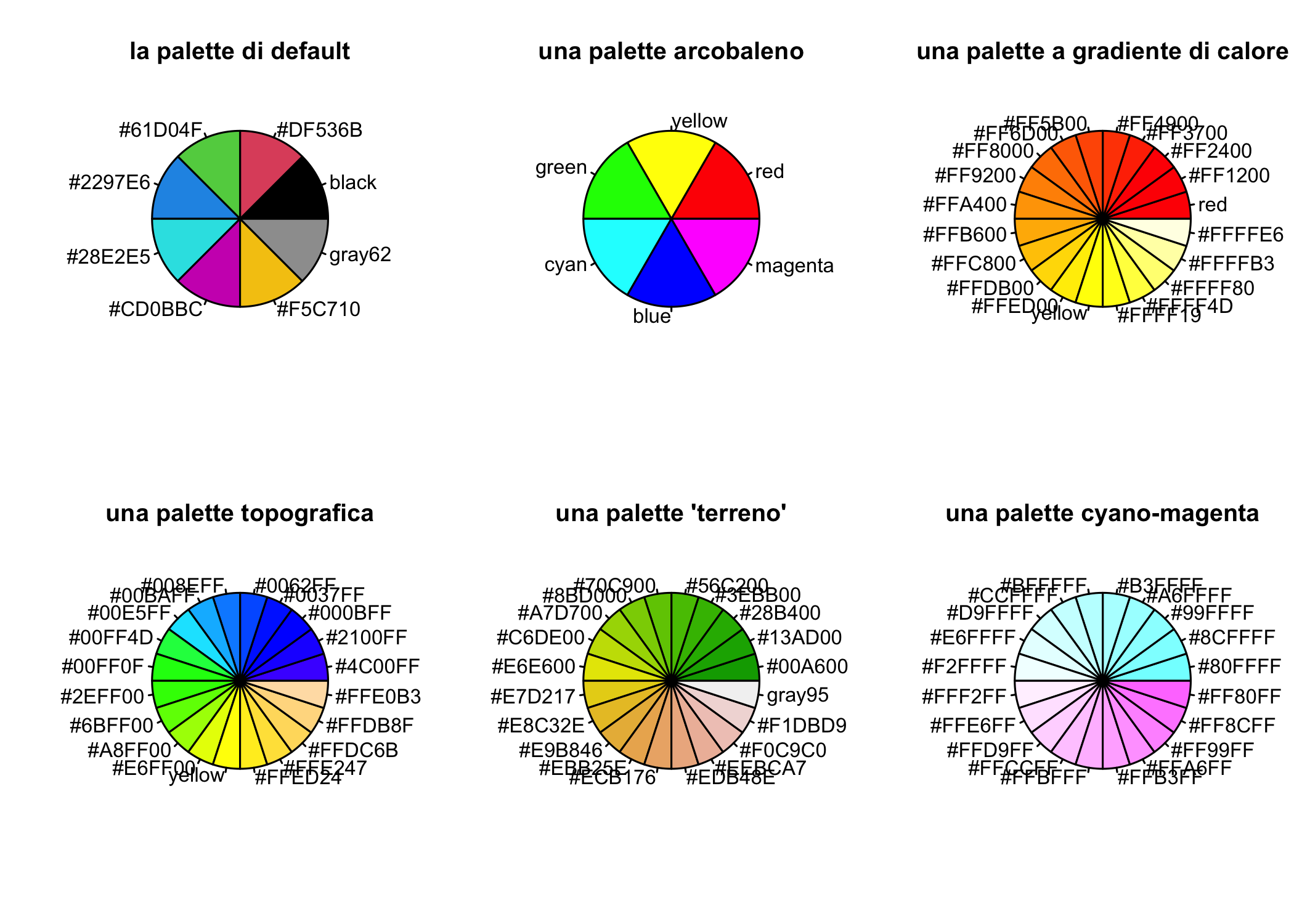
Figura 6.7: Sei palette di R rappresentate come diagrammi a torta.
Prova ad eseguire lo stesso codice con palette diverse.
RColorBrewer è un pacchetto che fornisce diverse palette ottimizzate per dati qualitativi e quantitativi (sequenziali o divergenti).
Per saperne di più scrivi nella console:
?RColorBrewerRColorBrewer fornisce molte palette ben fatte, ottimizzate anche per i diversi tipi di daltonismo.

Figura 6.8: Le palette di RColorBrewer.
6.6 La grammatica della grafica con ggplot2.
ggplot2 è sicuramente il sistema migliore, più flessibile e, probabilmente, più potente per produrre grafici scientifici in R. In più, il suo apprendimento è reso (relativamente) facile dall’organizzazione concettuale (creazione dei grafici in strati, usando i concetti della grammatica della grafica) e da un insieme di comandi dai nomi coerenti. Il materiale di riferimento per ggplot2 è disponibile qui e molti dei libri citati nella sezione 6.10 descrivono principalmente o esclusivamente la grafica con ggplot2.
La realizzazione di un grafico con ggplot2 inizia sempre con il comando ggplot ed è seguita da uno o più strati, separati dal segno +137, che definiscono gli altri elementi del grafico. Il risultato è una lista, che può essere assegnata ad un nome. Se non lo si fa, il comando genera immediatamente il grafico nel device attivo (in RStudio il plot pane). Se il grafico viene assegnato ad un nome è possibile continuare a modificarlo, aggiungendo ulteriori strati. In entrambi i casi, è possibile salvare facilmente il grafico con ggsave (vai al paragrafo 6.4.2 per dettagli).
La funzione qplot, che consentiva di produrre grafici molto rapidamente usando una sintassi vicina alla grafica di base, è ormai deprecata138, anche se è ancora possibile usare questo comando; qualche elemento lo trovi nel paragrafo 6.8.7.
La grammatica della grafica è una rappresentazione strutturata degli elementi che compongono un grafico (scientifico) e delle loro relazioni:
i dati: devono essere necessariamente sotto forma di
data frameotibble, vedi sezione 4.4, e possono essere “passati” tramite unapipe(%>%) o inseriti nella funzioneggplot139;gli “estetici” (aesthetics in inglese) definiscono quali variabili dei dati verranno assegnate a posizioni in un sistema di coordinate (x, y), ad altri elementi quantitativi (dimensione, trasparenza), ad elementi qualitativi come la forma dei simboli o la tipologia delle linee, ad elementi qualitativi o quantitativi come il colore;
i “geomi” (geoms in inglese) definiscono in che modo uno o più estetici vengono rappresentati (come grafico a barre, a dispersione, etc.) in uno strato (layer in inglese); lo strato eredita gli estetici dalla funzione
ggploto da uno strato precedente e, in alcuni casi, può utilizzare una trasformazione statistica o un aggiustamento di posizione (disposizione di elementi diversi che altrimenti si sovrapporrebbero nel grafico);le “annotazioni” (annotations in inglese) aggiungono uno strato con elementi fissi, come linee verticali, diagonali o orizzontali, mappe, etc.;
le “scale” (sia quelle quantitative che qualitative) possono essere generate automaticamente o personalizzate in maniera molto fine;
le “guide” di assi e legende servono al lettore ad interpretare correttamente un grafico; vengono generate automaticamente ma possono essere personalizzate in dettaglio (intervalli degli assi, trattini principali o secondari, etc.);
le “facet” servono per suddividere, sulla base di una o più variabili, il grafico in sub-grafici;
i “temi” (themes in inglese) consentono una personalizzazione molto fine di aspetti diversi del grafico (sfondo, colori delle guide, font, allineamento, etc.); esiste un gran numero di temi predefiniti e un certo numero di temi aggiuntivi forniti da pacchetti addizionali (come
ggthemes).
Descritto così, l’apprendimento di ggplot2 sembra un’impresa disperata. In realtà, nella maggior parte dei casi è possibile produrre grafici piacevoli ed efficaci con un minimo di opzioni: i default di ggplot2 sono “intelligenti” e spesso ggplot2 impedisce attivamente di fare cose sbagliate dal punto di vista della presentazione scientifica di dati (come per esempio produrre diagrammi a torte).
La figura 6.9 mostra un piccolo esempio che ci permette di individuare facilmente i diversi elementi.
# library(ggplot2)
mpg %>%
dplyr::filter(class %in% c("compact", "suv", "pickup", "subcompact")) %>%
ggplot(mapping = aes(x = displ, y = hwy)) +
geom_smooth(se = F) +
geom_smooth(method = "lm", formula = y~x, color = "red", linetype = 2, se = F) +
geom_point(mapping = aes(size = cyl, shape = class)) +
labs(
title = "Consumi in autostrada di alcuni modelli di autovetture, 1999 - 2008",
caption = "https://fueleconomy.gov/",
x = "cilindrata, litri",
y = "consumo in autostrada, km per gallone",
size = " n. cil.",
shape = "classe"
) +
scale_size(range = c(1,2.5)) +
scale_x_continuous(limits = c (1,7), breaks = seq(1,7), minor_breaks = seq(1,7,0.5)) +
scale_y_continuous(limits = c(10,50), breaks = seq(10,50,10), minor_breaks = seq(10,50,5)) +
scale_shape_manual( values = c(15, 16, 17, 18)) +
theme(title = element_text(hjust = 0.5))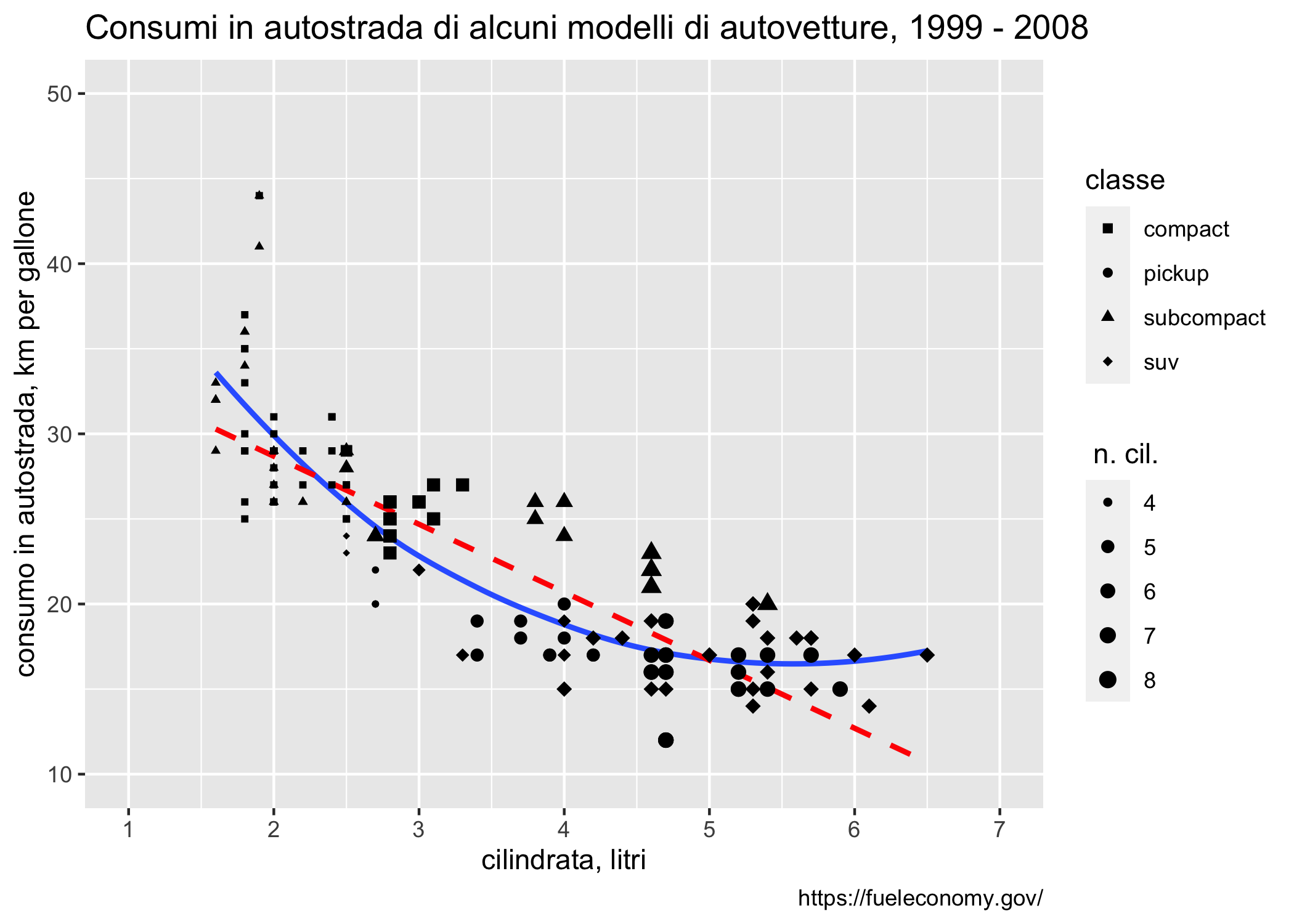
Figura 6.9: Gli elementi della grammatica della grafica in un grafico generato da ggplot
In questa figura:
i dati sono forniti dal database
mpg(filtrato), che viene “passato” al comandoggplot()con una pipe (%>%)gli estetici sono:
x = displ, y = hwy (indicati nella funzione
ggploted ereditati dagli strati successivi, rappresentano le coordinate nello spazio cartesiano)size = cyl (influenza la dimensione dei punti)
shape = class (influenza il tipo di simbolo utilizzato)
i geomi sono:
geom_smooth(passato due volte, con la creazione di uno strato con uno smoother non parametrico, in blu, e una regressione lineare, in rosso, con una linea tratteggiata)geom_point(che crea il grafico a dispersione)
alcune etichette sono modificate rispetto ai default con il comando
labsle scale sono modificate rispetto ai defaults con i comandi
scale_il tema utilizzato è quello di default, con una piccola modifica (allineamento del titolo al centro) ottenuta con il comando
theme
ggplot2 offre geomi adatti alla grande maggioranza dei grafici scientifici. In più, grafici più complessi e specializzati sono resi disponibili da altri pacchetti (le estensioni di ggplot2, vedi paragrafo 6.8.6). Imparare ad usarli tutti non è probabilmente necessario, anche se avere un’idea delle possibilità è utile e stimolante (vedi la sezione #ref(altrerisgraf)). Qui userò un approccio adatto a chi parte praticamente da 0, dividendo i comandi per generare grafici in due gruppi: quelli adatti alle sole variabili qualitative e quelli adatti alle variabili quantitative (se non ricordi cosa sono vai al paragrafo 4.1.2). In realtà, nel secondo caso si finisce spesso per usare combinazioni dei due tipi di variabili. Per semplicità, trascurerò alcuni tipi di grafici importanti, che saranno presentati in altri capitoli di questo testo (o di testi successivi, non ho ancora deciso).
6.7 Grafici per variabili qualitative.
Le variabili qualitative, e in particolare le variabili qualitative nominali, possono assumere solo valori discreti: per questo è possibile solo classificare i valori nei diversi gruppi e contarli. Le variabili qualitative sono spesso usate per individuare gruppi e per questo sono molto utilizzate nei grafici per variabili quantitative (vedi sezione 6.8). Di fatto, il tipo di grafico più comune per sole variabili qualitative è il grafico a barre140.
6.7.1 Diagrammi a barre.
In un grafico a barre si rappresentano tipicamente le conte o le proporzioni dei diversi livelli di una o più variabili qualitative. Come esempio, userò in set di dati Arthritis, disponibile nel pacchetto vcd. E’ un set di dati molto semplice, relativo ad un esperimento in cui, a gruppi diversi di pazienti, vengono somministrati un farmaco per il trattamento dell’artrite reumatoide o un placebo. Il set di dati ha 3 variabili qualitative (o fattori, Treatment, Sex, Improved, vedi paragrafo 4.1.2), una variabile quantitativa (Age) e un variabile (ID) che serve unicamente da identificativo del singolo paziente. Prima di procedere oltre, dovresti:
leggere l’aiuto del set di dati (prova con
?Arthritis)esplorare brevemente il set di dati usando le funzioni e i menu di RStudio o i comandi illustrati nel capitolo 4
cercare di capire cosa potrebbe essere interessante visualizzare in un grafico141
Prima di tutto, creerò un nuovo set di dati, con alcune piccole modifiche:
data("Arthritis")
# creo un fattore che divide in pazienti in tre gruppi usando la variabile Age,
# usando cut()
# i gruppi, arbitrariamente, sono con Age<=22, 22<Age≤40, 40<Age≤59, Age>59
Arthritis2 <- Arthritis
Arthritis2$ageClass <- cut(Arthritis2$Age,
c(22, 40, 59, max(Arthritis$Age)),
right = T,
labels = c("young","middle aged", "elder"))Qui e altrove, quando compare un comando che non conosci sarebbe prudente che tu ne leggessi, almeno superficialmente, l’aiuto. Non si sa mai, ti potrebbe essere utile in futuro…
Ora creo un semplice grafico a barre impilate (le conte dei gruppi definiti dalla variabile assegnata a fill sono impilati), che mostra l’effetto del trattamento sui sintomi. Nota come i dati rappresentino le conte dei diversi gruppi o combinazioni di gruppi (Treated x Improved). Dietro le quinte, geom_bar() usa la trasformazione stat_count() che tabula i valori delle diverse combinazioni.
# prima di tutto, creo una lista che può essere facilmente riciclata e che
# contiene i dati e solo un estetico, quello che andrà sull'asse delle x
artbar1 <- ggplot(data = Arthritis2, aes(x= Treatment))
# aggiungo il secondo strato con in geoma gem_bar, in cui passo un ulteriore
# estetico, Improved, che verrà mappato sul colore
artbar1 +
geom_bar(mapping = aes(fill = Improved))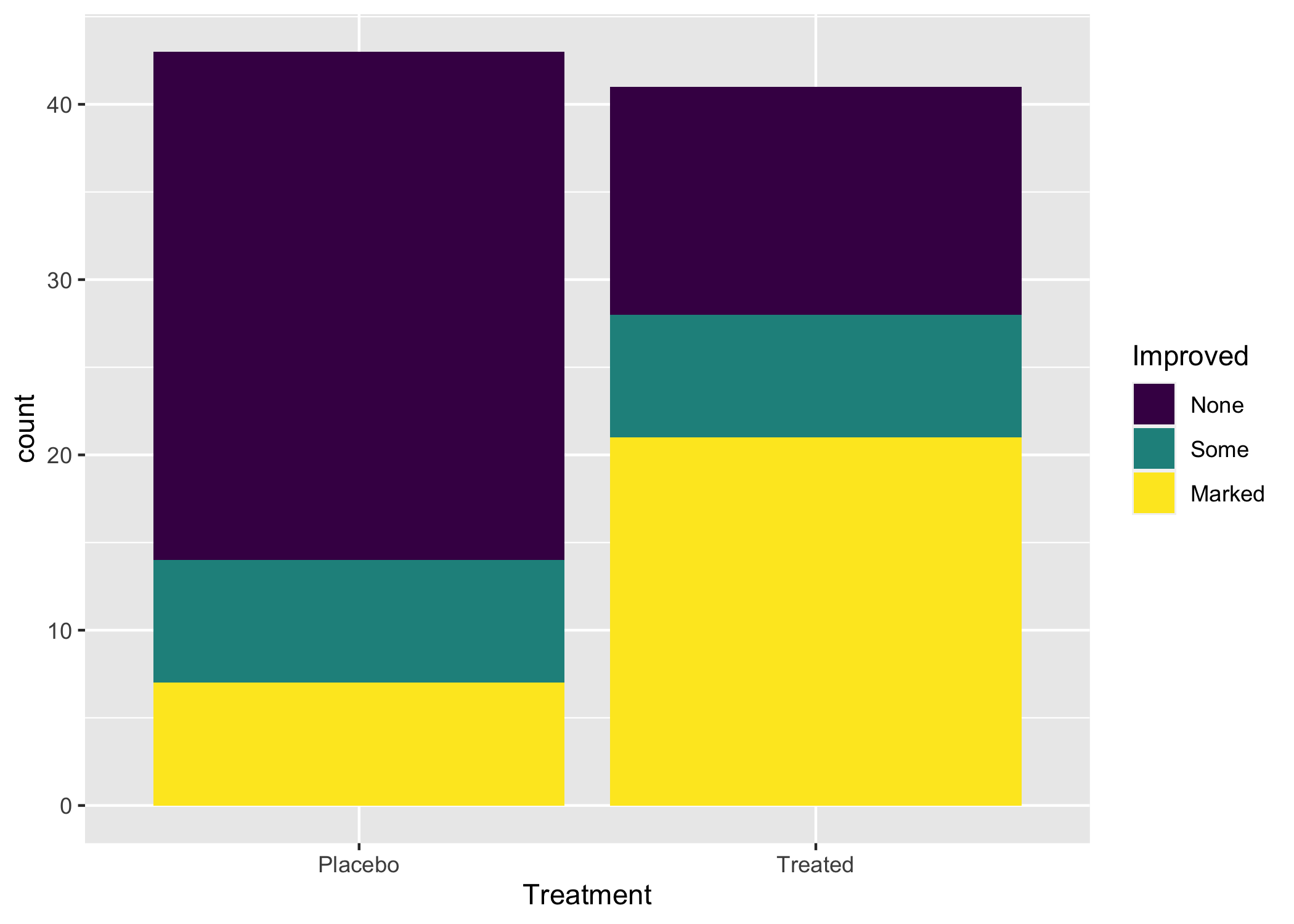
Figura 6.10: Un grafico a barre minimo.
Bene, semplice, no? La stessa cosa poteva essere realizzata con i seguenti comandi, che puoi copiare e incollare nella console:
ggplot(data = Arthritis2, aes(x= Treatment, fill = Improved)) +
geom_bar()Nota come il secondo strato, quello del geoma, “eredita” gli estetici dallo strato precedente.
Ora “migliorerò” un po’ il grafico, agendo su scale, colori, etichette, etc. Per farlo, parto comunque dal grafico creato in precedenza, che è nell’oggetto artbar1.
artbar_semplice <- artbar1 +
geom_bar(mapping = aes(fill = Improved))
# uso il comando labs per cambiare l'etichetta dell'asse y, aggiungere un
# titolo, sottotitolo e una legenda
artbar_semplice <- artbar_semplice +
labs(y = "Numero di pazienti",
title = "Effetto del farmaco x sui sintomi dell'artrite reumatoide",
subtitle = "Un esperimento randomizzato, con placebo e doppio cieco",
caption = "Koch & Edwards, 1988")
# cambio le scale, per usare termini in Italiano, aggiungere dei trattini
# diversi per l'asse y e cambiare la palette dei colori
artbar_semplice <- artbar_semplice +
scale_x_discrete("Trattamento",
labels = c("Placebo" = "Placebo", "Treated" = "Farmaco x")) +
scale_y_continuous(limits = c(0, 50), breaks = seq(0,50,10),
minor_breaks = seq(0,50,2)) +
scale_fill_brewer("Miglioramenti",
labels = c("None" = "0","Some"="+", "Marked" = "+++"),
type = "qual", palette = "Paired")
# cambio il tema, e centro i titoli, cambiandone font e dimensione
artbar_semplice <- artbar_semplice +
theme_bw() +
theme(plot.title = element_text(hjust = 0.5, face = "bold"),
plot.subtitle = element_text(hjust = 0.5, face = "italic", size = 12))
artbar_semplice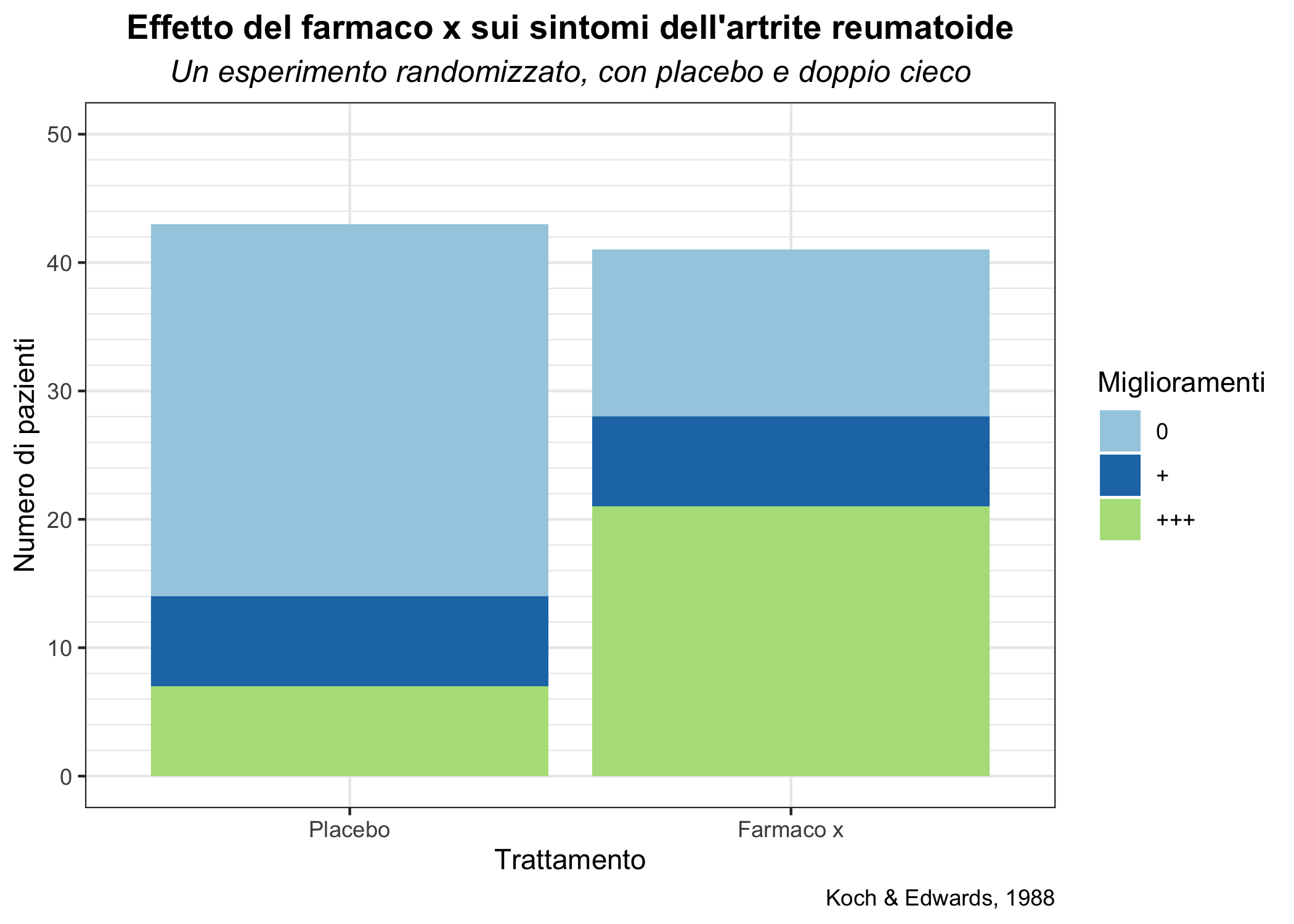
Figura 6.11: Un grafico a barre semplice.
Nota come:
avrei potuto produrre il grafico aggiungendo i vari strati in un solo comando multilinea, oppure tenere uno strato di base, con gli elementi minimi cui aggiungere le personalizzazioni
tutti gli elementi passati ai comandi
labsescalepotevano essere definiti “esternamente” al comando, p.es. usando dei vettori con (nell’opzione labels discale_x_discrete) o senza nomi (negli altri casi); ciascuno di questi elementi poteva essere persino il risultato di una funzionebenché si possa personalizzare praticamente tutto, con pochissimi comandi è possibile usare un grafico accettabile e gradevole
Prova tu stess*!
Ora, consentimi una piccola digressione. Dirai tu, se posso ottenere un buon risultato con pochi comandi o, meglio ancora, usando un software con un’interfaccia “punta e clicca”, perché devo fare tutta questa fatica ad imparare ad usare R e ggplot2? È un’ottima domanda, ma ti consiglio di rileggere bene l’introduzione a questo testo (capitolo 1). Inoltre, i grafici realizzati con R hanno due caratteristiche fondamentali per la scienza moderna: la trasparenza (è sempre molto chiaro cosa hai fatto per ottenere un grafico) e la riproducibilità (chiunque, anche su un’altra piattaforma, può riprodurre esattamente lo stesso grafico). Infine (e questo credo sia un buon argomento), se un revisore maligno ti chiede di modificare un grafico è molto più facile farlo se lo hai realizzato con R.
Per cambiare la disposizione del grafico a barre è possibile usare l’argomento position in geom_bar: Nella figura 6.12 ho usato i tre possibili valori:
stack, il default, produce diagrammi a barre impilate: hanno il vantaggio di permettere di confrontare facilmente i valori delle categorie definite dalla variabile cui è stato attribuito il riempimento (fill)142 comeaesthetic, ma, quando la conta dei valori per le categorie definite dall’asse delle x è molto diversa diventa difficile confrontare l’effetto della variabile assegnata all’asse delle x su quella assegnata alfilldodge: produce diagrammi a barre affiancate: anche in questo caso, mentre è facile il confronto delle diverse categorie all’interno di uno stesso gruppo definito da un valore sull’asse delle x, non è altrettanto facile confrontare l’effetto della variabile sull’asse delle x sulla distribuzione della variabile assegnata al riempimento; rispetto astackè possinbile ottenere con maggiore precisione i singoli valori per le diverse categorie definite dalfill;fill: comestack, ma i valori della variabile assegnata al riempimento sono visualizzati come proporzioni (tutte le barre hanno altezza uguale e, se non lo si aggiunge come etichetta, è impossibile conoscere il valore della conta per ogni dato valore di x); utile quando l’enfasi è sul confronto di proporzioni;
Nota inoltre come questa figura sia in realtà costruita affiancando 3 diversi elementi grafici usando la funzione plot_grid() del pacchetto cowplot143. Questo è molto diverso dal creare pannelli in un grafico usando un’altra variabile, come vedremo dopo per l’uso di facet_wrap e facet_grid. Inoltre, in tutti e tre i grafici la legenda è stata spostata sul fondo del grafico. Prova a esplorare altre posizioni della legenda. Nota anche come la legenda sia stata soppressa in due grafici e personalizzata in quello centrale.
barre_impilate <- artbar1 +
geom_bar(mapping = aes(fill = Improved)) +
labs(y = "Numero di pazienti") +
scale_x_discrete("Trattamento",
labels = c("Placebo" = "Placebo", "Treated" = "Farmaco x")) +
scale_fill_brewer("Miglioramenti",
labels = c("None" = "0","Some"="+", "Marked" = "+++"),
type = "qual", palette = "Paired") +
theme(plot.title = element_text(hjust = 0.5, face = "bold"),
plot.subtitle = element_text(hjust = 0.5, face = "italic", size = 12),
legend.position = "none")
barre_raggruppate <- artbar1 +
geom_bar(mapping = aes(fill = Improved), position = "dodge") +
labs(y = "Numero di pazienti") +
scale_x_discrete("Trattamento",
labels = c("Placebo" = "Placebo", "Treated" = "Farmaco x")) +
scale_fill_brewer("Miglioramenti",
labels = c("None" = "0","Some"="+", "Marked" = "+++"),
type = "qual", palette = "Paired") +
theme(plot.title = element_text(hjust = 0.5, face = "bold"),
plot.subtitle = element_text(hjust = 0.5, face = "italic", size = 12),
legend.position = c(0.50,0.85), legend.text = element_text(size = 6))
barre_proporzioni <- artbar1 +
geom_bar(mapping = aes(fill = Improved), position = "fill") +
labs(y = "Frazione dei pazienti") +
scale_x_discrete("Trattamento",
labels = c("Placebo" = "Placebo", "Treated" = "Farmaco x")) +
scale_fill_brewer("Miglioramenti",
labels = c("None" = "0","Some"="+", "Marked" = "+++"),
type = "qual", palette = "Paired") +
theme(plot.title = element_text(hjust = 0.5, face = "bold"),
plot.subtitle = element_text(hjust = 0.5, face = "italic", size = 12),
legend.position = "none")
plot_grid(barre_impilate, barre_raggruppate, barre_proporzioni,
labels = c("A", "B", "C"),
ncol = 3, nrow = 1)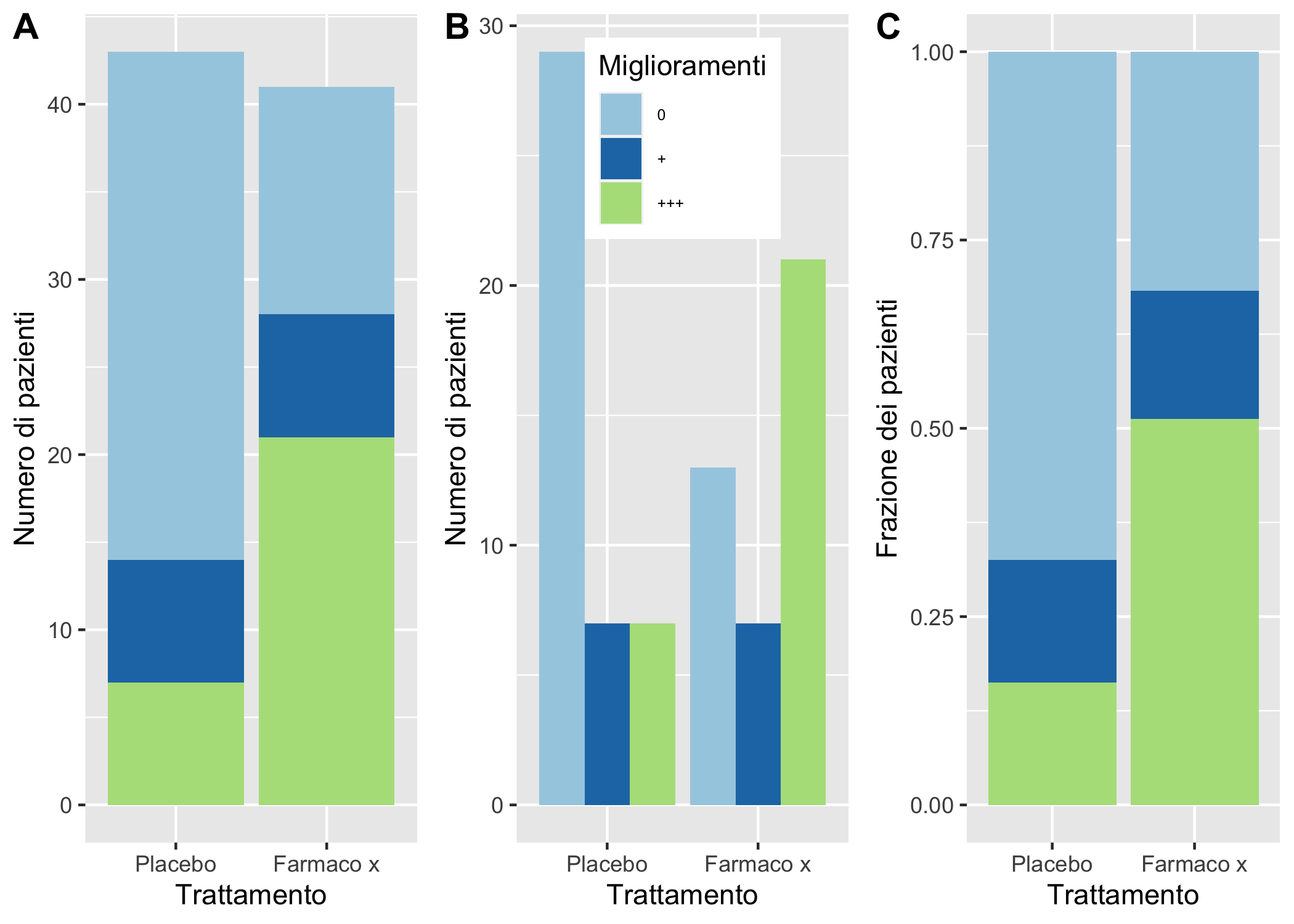
Figura 6.12: L’uso dell’argomento position nei diagrammi a barre.
In tutti e tre i grafici è evidente come l’uso del farmaco x, rispetto al placebo, incrementi il numero dei casi con un marcato miglioramento dei sintomi e diminuisca il numero dei casi con sintomi gravi, anche se questo effetto è molto più evidente nel grafico C, dove l’altezza delle colonne è standardizzata.
Nota come il codice sia molto verboso (moltissime linee di codice per ottenere il grafico desiderato) e come i grafici B e C siano stati ottenuti, di fatto, facendo un copia e incolla del codice del primo grafico e modificando due elementi (l’argomento position di geom_bar e la legenda dell’asse delle y). Questa pratica, oltre che essere inelegante, è soggetta ad errore. Una soluzione più elegante è definire una funzione (vedi capitolo 4, paragrafo 4.10.4).
Prova tu stesso con il codice che segue: è sufficiente cambiare gli argomenti bpos, yl e lpos della funzione per ottenere l’effetto desiderato:
Genera_bar_plot <- function(bpos = "stack",
yl = "Numero di pazienti",
lpos = "right"){
artbar1 +
geom_bar(mapping = aes(fill = Improved), position = bpos) +
labs(y = yl) +
scale_x_discrete("Trattamento",
labels = c("Placebo" = "Placebo", "Treated" = "Farmaco x")) +
scale_fill_brewer("Miglioramenti",
labels = c("None" = "0","Some"="+", "Marked" = "+++"),
type = "qual", palette = "Paired") +
theme(plot.title = element_text(hjust = 0.5, face = "bold"),
plot.subtitle = element_text(hjust = 0.5, face = "italic", size = 12),
legend.position = lpos)
}
# cambia gli argomenti della funzione fra parentesi;
# yl può essere qualsiasi testo,
# bpos può essere "stack", "dodge" o "fill"
# lpos può essere "bottom", "top", "right", "left"
# o un vettore numerico di lunghezza 2
# che definisce la posizione della legenda
# qui vengono usati gli argomenti di default
il_mio_bar_plot <- Genera_bar_plot()
il_mio_bar_plot
# qui invece viene generato l'equivalente del grafico C nella figura precedente,
il_mio_bar_plot <- Genera_bar_plot(bpos = "fill",
yl = "frazione dei pazienti",
lpos = "bottom")
il_mio_bar_plotDividere i grafici in subplot usando un’ulteriore variabile qualitativa può essere utile. Nella Figura 6.13 è possibile apprezzare come pazienti di sesso femminile o maschile reagiscano diversamente al trattamento farmacologico.
Il grafico include anche le seguenti personalizzazioni:
le etichette dei pannelli, che dovrebbero corrispondere ai livelli della variabile
Sexsono state cambiate;il numero totale di casi per ciascuna barra impilata a proporzioni è stato aggiunto con
geom_text
i_nomi_dei_sessi <- as_labeller(
c("Female" = "Femmine", "Male" = "Maschi"))
ggplot(data = Arthritis2, aes(x= Treatment)) +
geom_bar(mapping = aes(fill = Improved), position = "fill") +
geom_text(aes(label = after_stat(count)), stat = "count",
position = "fill", colour = "white", vjust = 1.5) +
facet_wrap(~Sex, labeller = i_nomi_dei_sessi) +
labs(y = "Frazione dei pazienti") +
scale_x_discrete("Trattamento",
labels = c("Placebo" = "Placebo", "Treated" = "Farmaco x")) +
scale_fill_brewer("Miglioramenti",
labels = c("None" = "0","Some"="+", "Marked" = "+++"),
type = "qual", palette = "Paired") +
theme(plot.title = element_text(hjust = 0.5, face = "bold"),
plot.subtitle = element_text(hjust = 0.5, face = "italic", size = 12))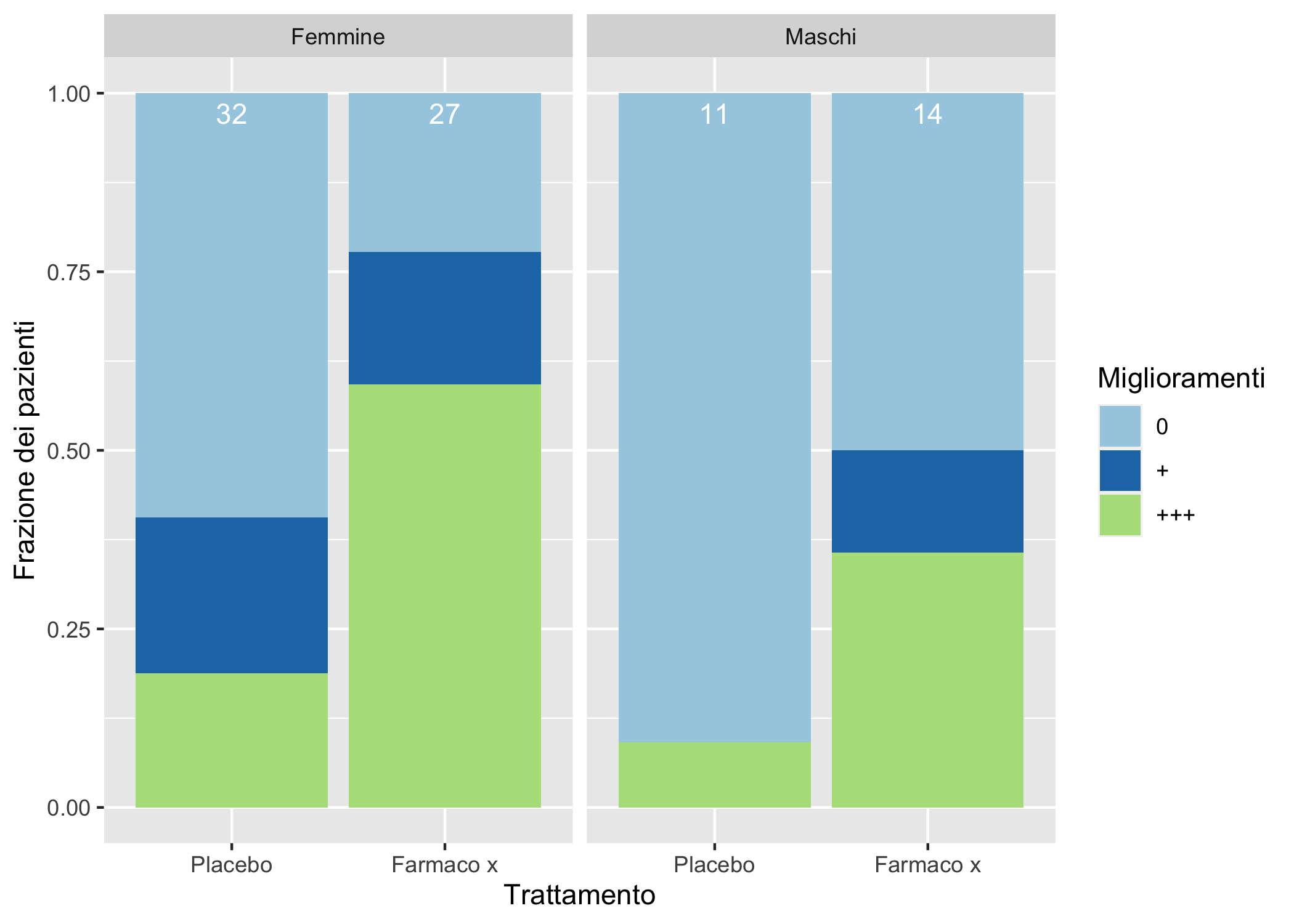
Figura 6.13: Un grafico a barre con facet
La presenza dei numeri indica abbastanza chiaramente che l’esperimento è sbilanciato, con un numero di pazienti di sesso femminile molto più alto. E’ anche abbastanza chiaro perché sia necessario un esperimento con doppio cieco e placebo per testare un farmaco ;-)
Incidentalmente, potrebbe essere interessante l’età dei pazienti come ulteriore variabile. Prova tu stess* a creare un grafico con il dataset Arthritis2 usando facet_grid(Sex ~ ageClass).
Arthritis2 %>% ggplot(mapping = aes(x=Treatment, fill = Improved)) +
facet_grid(Sex ~ ageClass) +
geom_bar()6.7.2 Fare di più con i grafici per variabili qualitative.
Il grafico a barre è sicuramente il grafico più efficace per rappresentare conte di variabili qualitative. I blocchi di codice successivo, che devi eseguire in uno script o nella console, ti permettono di sperimentare con alcune personalizzazioni utili.
Trasporre gli assi può essere utile quando le etichette dell’asse delle x sono piuttosto lunghe:
artbar1 + geom_bar(aes(fill = Improved)) + coord_flip()Esplora l’aiuto di theme per vedere come, con axis.text.x (o le funzioni equivalenti con gli altri elementi di testo del grafico) e element_text() è possibile personalizzare posizione, angolo, giustificazione delle etichette. Grafici trasposti possono essere ottenuti con il pacchetto estensione ggstance.
ggplot2 non consente in maniera semplice di creare diagrammi a torta (pie charts), probabilmente perché sono uno dei tipi peggiori di rappresentazione dei dati. E’ possibile creare qualcosa di simile usando le coordinate polari:
artbar1 + geom_bar(aes(fill= Improved), show.legend = F) + coord_polar()Oppure, se veramente sei testard*, prova i suggerimenti forniti da “R graphical cookbook” (vedi in altre risorse ***) o il pacchetto ggpie. O, ancora potresti provare i fan plot (plotrix::fan.plot()) o provare qualche alternativa, come i doughnut plot (grafici a ciambella), per esempio usando i pacchetti ggsector o ggpie.
Altri tipi di grafici per variabili qualitative interessanti sono:
i diagrammi a mosaico (clicca qui per qualche esempio o prova con ggmosaic)
i treemaps con il pacchetto specializzato
treemapo con treemapify
6.8 Grafici per variabili quantitative.
Spesso ci interessa rappresentare la distribuzione o le relazioni fra una o più variabili quantitative, magari anche in funzione dei gruppi determinati dai livelli di una o più variabili qualitative.
Le rappresentazioni grafiche per queste situazioni sono varie, e possono essere combinate:
rappresentazioni della distribuzione o densità
gli istogrammi (histogram) sono una versione continua dei diagrammi a barre: l’intervallo di valori di una singola variabile quantitativa viene diviso in un certo numero di intervalli più piccoli, di solito di uguali dimensioni; l’altezza delle barre per ciascun intervallo mostra la conta dei valori di ciascun gruppo. In questo caso (
geom_histogram) è sufficiente una sola variabile x quantitativa (l’asse delle y mostra le conte), mentre altre variabili qualitative possono essere utilizzate per il colore dei bordi o il riempimento delle barre; è anche possibile ottenere equivalenti bi- o tridimensionali per 2 variabili quantitative (geom_bin2dogeom_hex) in cui l’intensità o la gradazione del colore rappresenta il numero di osservazioni per ciascuna combinazione di intervalli x e y;i poligoni di frequenza (frequency polygon,
geom_freqpoly) o i diagrammi ad area (area plot,geom_area) sono due buone alternative agli istogrammi per la stessa tipologia dei dati, e usano rispettivamente una linea spezzata o un’area per rappresentare la distribuzione; analogamente agli istogrammi, colori dei bordi o riempimenti possono essere usati per mostrare l’effetto di variabili qualitative;i grafici a densità (
geom_density) usano qualche sorta di approssimazione continua (smoother) per rappresentare la densità; anche per questi esistono equivalenti a due dimensioni;i box plot, ottenuti con
geom_boxplot, e il loro analogo continuo, i violin plot (geom_violin) sono utili a rappresentare, in modo non parametrico (cioé senza fare ipotesi particolari sui parametri della distribuzione), la distribuzione di una variabile quantitativa (y) in funzione di uno o più valori di una variabile qualitativa (x)con qualche accorgimento, alcuni altri geomi (
geom_point,geom_jitter,geom_rug) possono essere utilizzati, spesso in combinazione con altri geomi, per rappresentare densità e distribuzione di variabili quantitative
rappresentazioni di indicatori di tendenza centrale e della relativa incertezza o variabilità: in molti casi è interessante riassumere una distribuzione unimodale rappresentandone qualche indicatore di tendenza centrale (media, mediana) con qualche indicatore di variabilià o incertrezza (deviazione standard, range interquartile, intervalli di confidenza). In genere, questi grafici hanno un’asse delle x qualitativo (diverse categorie di una variabile qualitativa) e una y quantitativa. Oltre ai boxplot, già descritti in precedenza, è possibile usare:
diagrammi a rettangoli con barre di confidenza (
geom_colcombinato congeom_errorbarogeom_linerange)diagrammi a punti e barre di errore (
geom_pointrange, o una combinazione digeom_pointegeom_linerange), eventualmente rappresentati come rettangoli (geom_crossbar)
rappresentazione delle relazioni quantitative fra 2 o più variabili quantitative (correlazione, relazione funzionale) o qualitative (distribuzione in gruppi):
grafici a dispersione (scatterplot,
geom_point), arricchiti con una varietà di altri elementi (colore, dimensione e forma dei punti) sono letteralmente il cavallo da lavoro della grafica scientifica e possono essere combinati con altre rappresentazioni (come le curve di interpolazione, gli smoothers, le curve di regressione)annotazioni rappresentanti l’andamento della relazione fra due variabili possono essere ottenute con geom_smooth che permette di usare smoothers parametrici e non parametrici o linee di regressione
annotazioni rappresentanti la distribuzione bivariata possono essere ottenute con
stat_ellipse(che permette di ottenere ellissi di confidenza) estat_density2d
6.8.1 Istogrammi e altre rappresentazioni della densità.
In molti casi, quello che ci interessa è mostrare la distribuzione di una singola variabile continua, per mostrarne i valori più frequenti, il range e, in qualche caso, per verificare se, in realtà si tratti di una distribuzione di valori estratti da più di una popolazione. Per costruire un istogramma l’intervallo dei valori viene diviso in tanti piccoli contenitori (bin), delimitanti intervalli più piccoli, di solito di dimensioni uguali, e si contano le osservazioni che ricadono in ogni singolo contenitore. Ovviamente, ha poco senso farlo quando si dispone di poche osservazioni (diciamo <20). D’altra parte, quando si dispone di moltissime osservazioni potrebbe essere opportuno usare approssimazioni a distribuzioni continue, che potrebbero mostrare meglio la forma della distribuzione. Per questa piccola dimostrazione (e per altre relative alle distribuzioni di densità) userò alcuni data set:
ggplot2::mpgggplot1::diamondsdatasets::irisMASS::survey
Puoi usare l’aiuto per saperne di più.
Cominciamo con i diamanti (i migliori amici delle ragazze). Prova, da sol*, a leggere l’aiuto di questo data set. Nel frattempo ecco la distribuzione del peso di circa 50.000 diamanti in carati. Nota come nella Figura 6.14 ho cambiato il valore di default del numero di bin (da 30 a 1000)
data("diamonds")
dfpoly <- ggplot(data = diamonds, aes(x=carat))
dfpoly + geom_histogram(bins = 100) +
labs(x = "peso in carati",
y = "conta",
title = "distribuzione del peso in carati di diamanti") +
theme(plot.title = element_text(hjust = 0.5, face = "bold"))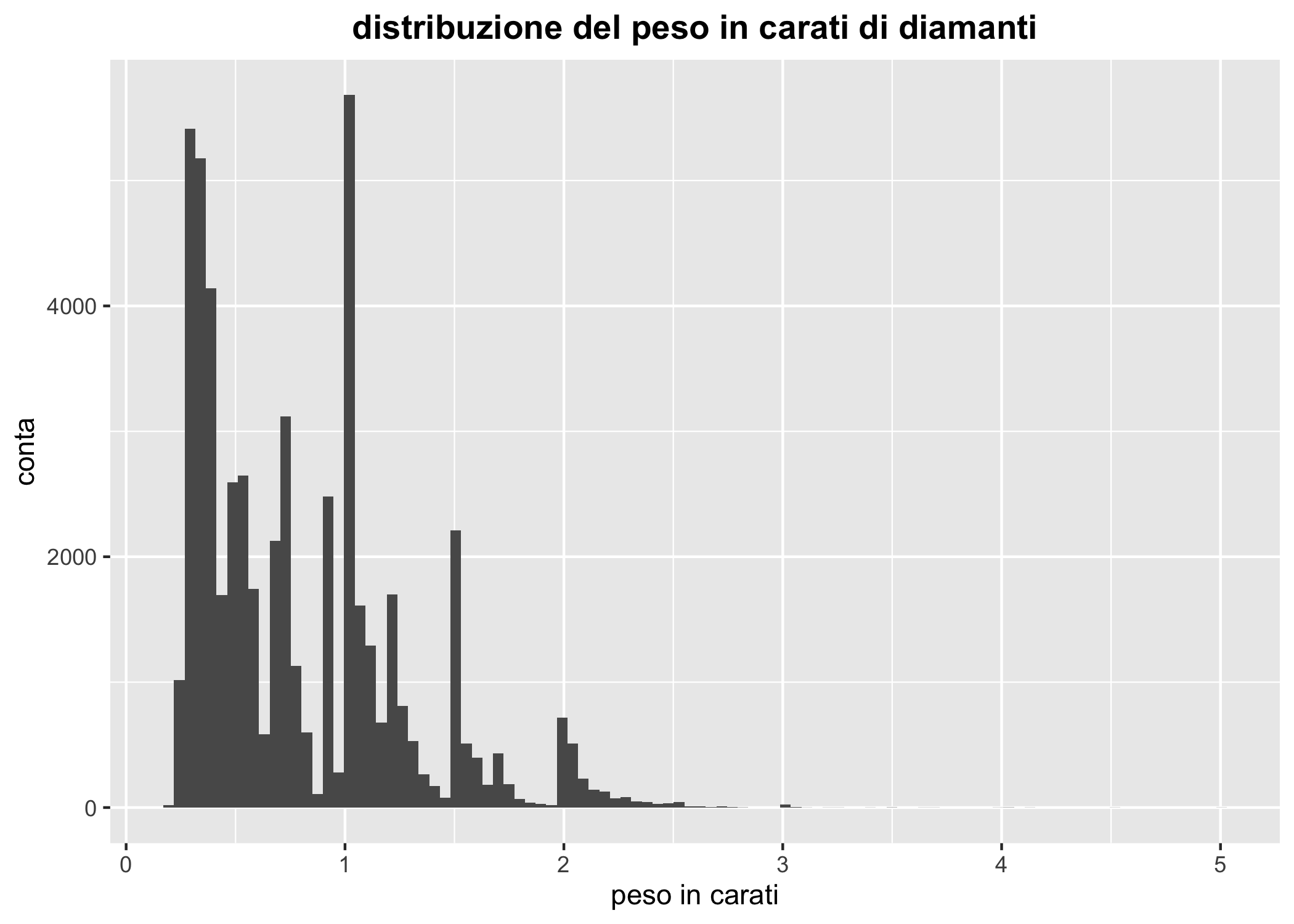
Figura 6.14: Un istogramma mostrante la distribuzione del peso in carati di oltre 50000 diamanti
La figura non è molto informativa: la scala dell’asse delle x è molto lunga ma, dato il numero ridottissimo di diamandi di grandi dimensioni è difficile apprezzare bene la distribuzione, anche se è chiaro che ci sono diverse sottopopolazioni. Una soluzione, in questo caso, potrebbe essere quella di trasformare uno degli assi. Prova questo piccolo trucco, che ti consente di usare una scala logaritmica per l’asse delle y e, contemporaneamente di usare dei tickmark appropriati144.
dfpoly + geom_histogram(bins = 100) +
labs(x = "peso in carati",
y = "conta",
title = "distribuzione del peso in carati di diamanti") +
scale_y_log10() +
theme(plot.title = element_text(hjust = 0.5, face = "bold"))Noterai come il risultato è po’ meglio e un po’ peggio: trasformare le scale può rendere più difficile l’interpretazione, ma almeno qui si vedono i valori delle conte dei diamanti più grandi (una gran bella soddisfazione). Ovviamente, si può fare di meglio: possiamo annotare meglio le scale, cambiarne lo stile e usare un tema diverso (così iniziamo a fare pratica con le annotazioni).
dfpoly + geom_histogram(bins = 100) +
labs(x = "peso in carati",
y = "conta",
title = "distribuzione del peso in carati di diamanti") +
scale_y_log10(limits = c(1,10^4), breaks = scales::trans_breaks("log10", function(x) 10^x),
labels = scales::trans_format("log10", scales::math_format(10^.x))) +
scale_x_continuous(breaks = seq(0,5,0.5), minor_breaks = seq(0,5,0.1)) +
annotation_logticks(sides = "l") +
theme_bw() +
theme(plot.title = element_text(hjust = 0.5, face = "bold"))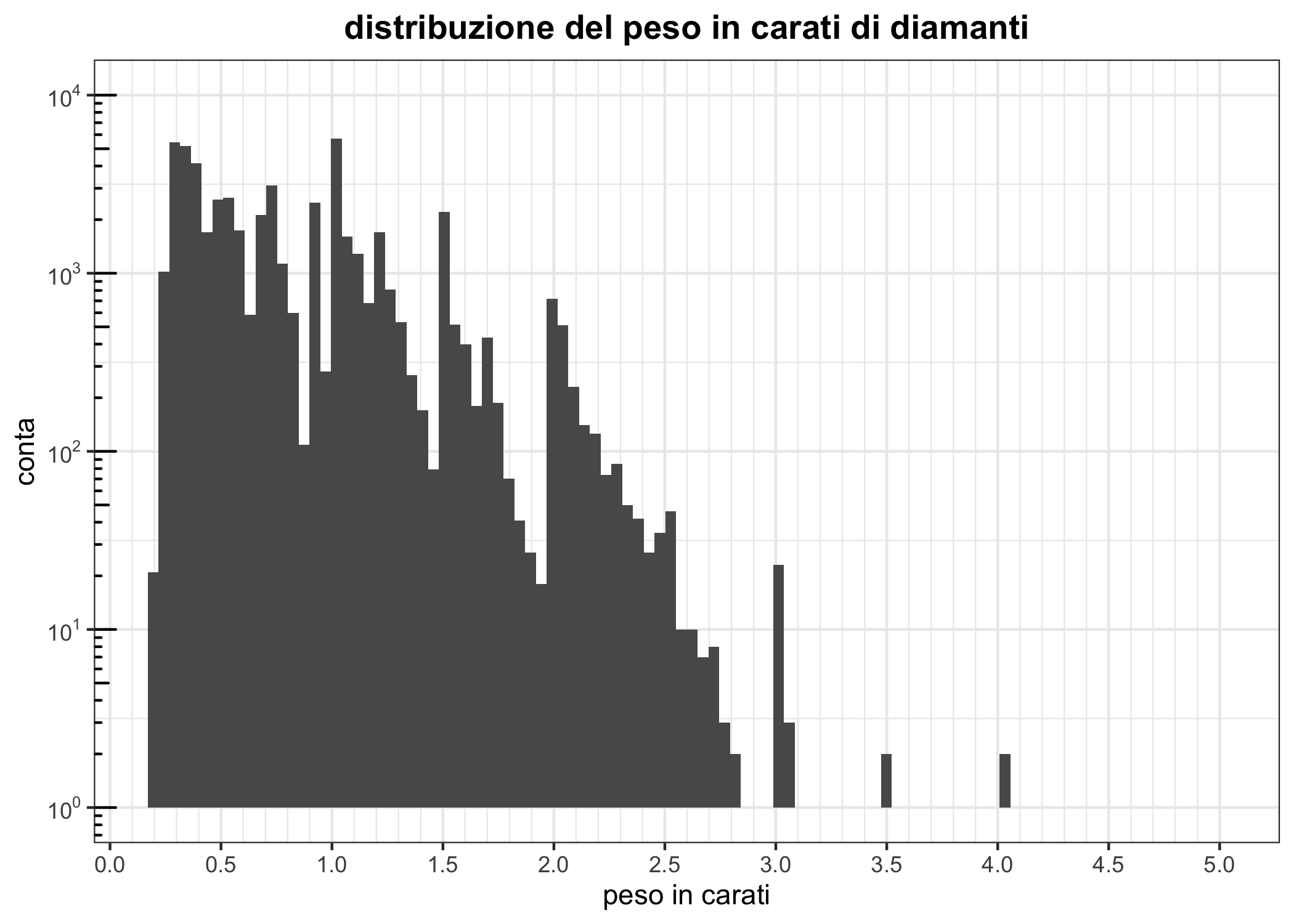
(#fig:log_carat_histo_2)Uso di scale logaritmiche: un’istogramma della dimensione di diamanti in carati.
Prova qui per saperne molto di più sulle annotazioni di scale trasformate.
Naturalmente, geom_histogram() capisce molti altri estetici, come fill e alpha. Prova questo codice che vedere anche la distribuzione del taglio (cut):
dfpoly + geom_histogram(aes(fill = cut), bins = 100) +
labs(x = "peso in carati",
y = "conta",
fill = "taglio",
title = "distribuzione del peso in carati di diamanti") +
scale_y_continuous(limits = c(0,6000), minor_breaks = seq(0,6000,200)) +
scale_x_continuous(breaks = seq(0,5,0.5), minor_breaks = seq(0,5,0.1)) +
theme_bw() +
theme(plot.title = element_text(hjust = 0.5, face = "bold"))Oppure, prova ad aggiungere delle facet
dfpoly + geom_histogram(bins = 100) +
facet_grid(cut ~ clarity) +
labs(x = "peso in carati",
y = "conta",
fill = "taglio",
title = "distribuzione del peso in carati di diamanti, in funzione di taglio e chiarezza") +
theme_bw() +
theme(plot.title = element_text(hjust = 0.5, face = "bold"))Un’applicazione interessante è aggiungere una funzione di densità teorica di probabilità all’istogramma. Proviamo con dei dati biologici, come l’altezza di studenti (che è più probabile siano normalmente distribuita). Qui usiamo MASS::survey. Qui ho anche aggiunto linee che mostrano la media (linea verticale continua) e ±sd (deviazione standard, linee tratteggiate).
data("survey")
male_students <- dplyr::filter(survey, Sex == "Male" & !is.na(Height))
ggplot(male_students) +
geom_histogram(aes(x = Height, y = after_stat(density)), bins = 10) +
stat_function(fun = dnorm,
args = list(mean = mean(male_students$Height),
sd = sd(male_students$Height))) +
geom_vline(xintercept = mean(male_students$Height)) +
geom_vline(xintercept = c(mean(male_students$Height)-sd(male_students$Height),
mean(male_students$Height)+sd(male_students$Height)),
linetype = I(2)) +
labs(x = "altezza, cm",
y = "densità") +
theme_bw()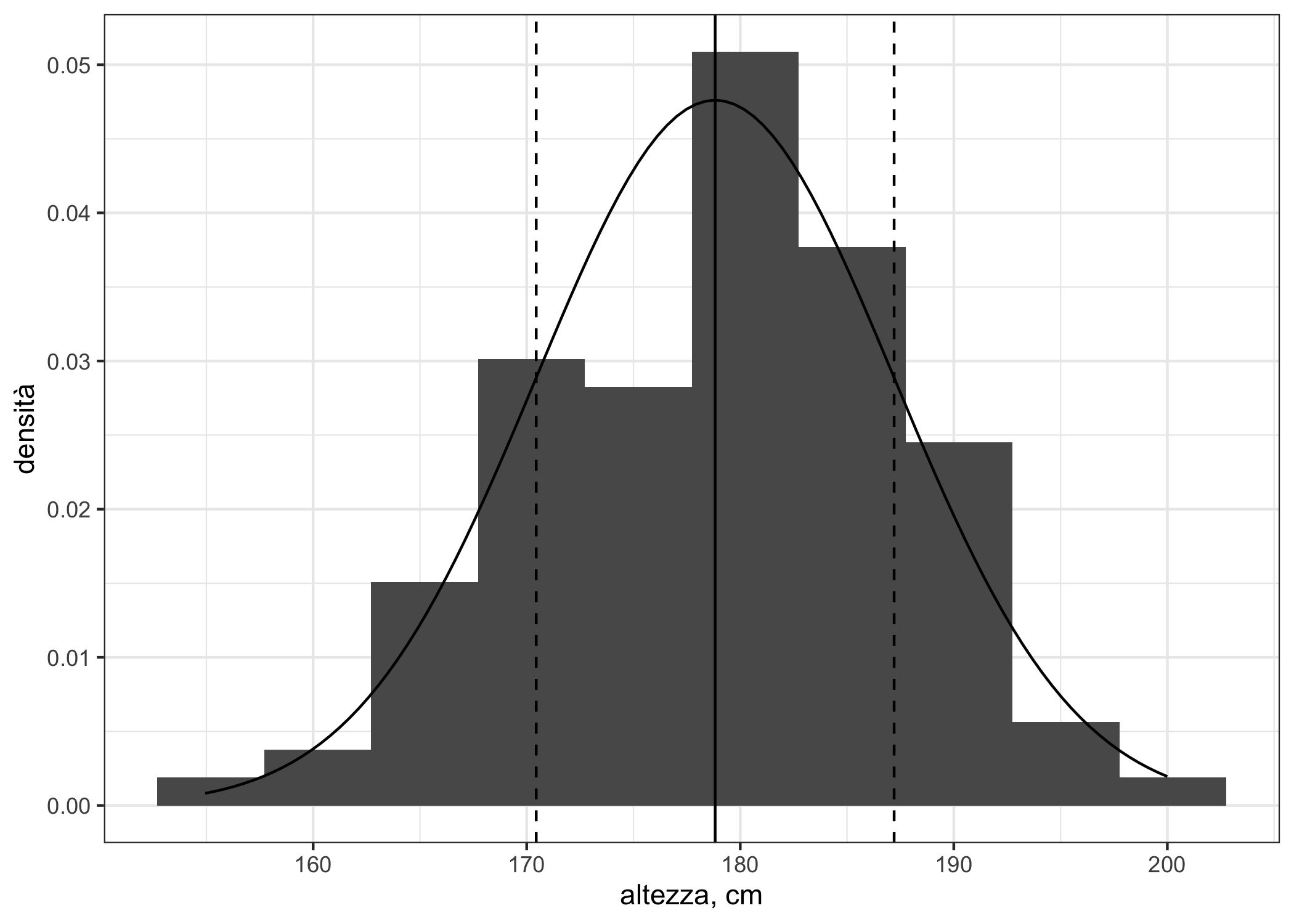
(#fig:isto_norm)Istogramma e funzione di densità di probabilità per l’altezza di studenti universitari di sesso maschile
Un’alternativa agli istogrammi sono i poligoni di frequenza. Il principio è lo stesso ma, invece di avere una serie di barre, una linea spezzata collega i punti corrispondenti alla conta delle osservazioni per ogni bin. Un vantaggio rispetto agli istogrammi è che è più facile sovrapporre diversi gruppi, magari usando colori diversi.
dfpoly <- ggplot(data = diamonds, aes(x=carat))
dfpoly + geom_freqpoly(aes(colour = cut)) +
ggtitle("Distribuzione del peso di diamandi, carati, per diamanti con qualità di taglio diverso") +
labs(x = "carati", y = "conta") +
scale_colour_brewer(type = "qual", palette = "Dark2") +
theme_bw() +
theme(plot.title = element_text(hjust = 0.5, face = "bold"))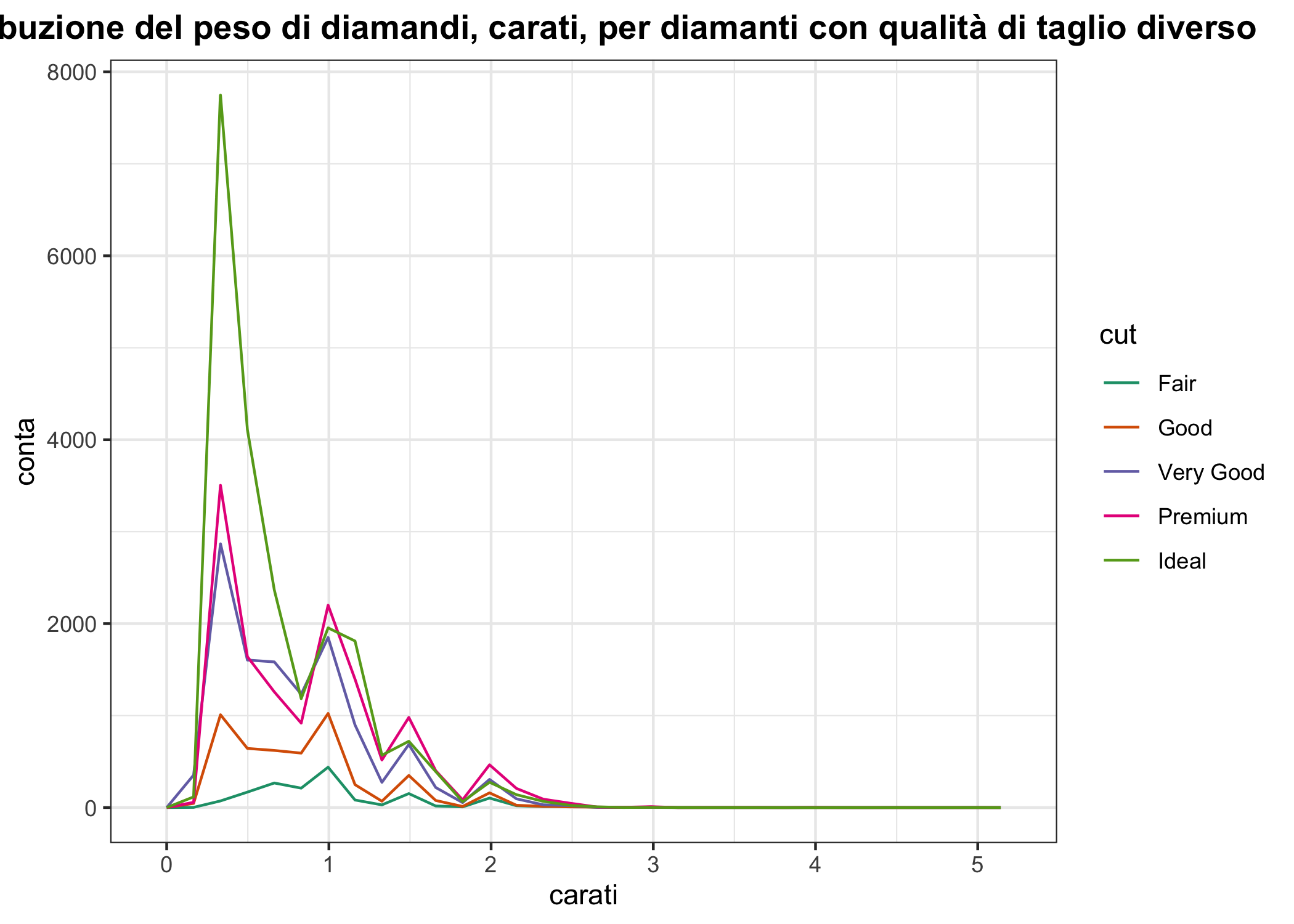
Figura 6.15: Un esempio di poligoni di frequenza (la distribuzione del peso di diamanti di tagli diversi)
Invece dei poligoni di frequenza (che al massimo possono usare linee di diverso colore, spessore o stile) è possibile usare grafici ad area (che possono usare riempimenti diversi). Nota che in questo caso stat = "bin" è usato per ottenere conte corrispondenti ai vari bin e position="stack" è usato per impilare le conte. Prova a chiederti come è stato ottenuto l’ordine dei diversi livelli del taglio (cut). Prova anche, che non guasta mai, ad interpretare il grafico.
dfpoly + geom_area(aes(fill= cut), stat = "bin", position = "stack") +
ggtitle("Distribuzione del peso di diamandi, carati, in funzione del taglio") +
labs(x = "carati", y = "conta") +
scale_fill_brewer(type = "qual", palette = "Dark2") +
theme_bw() +
theme(plot.title = element_text(hjust = 0.5, face = "bold"))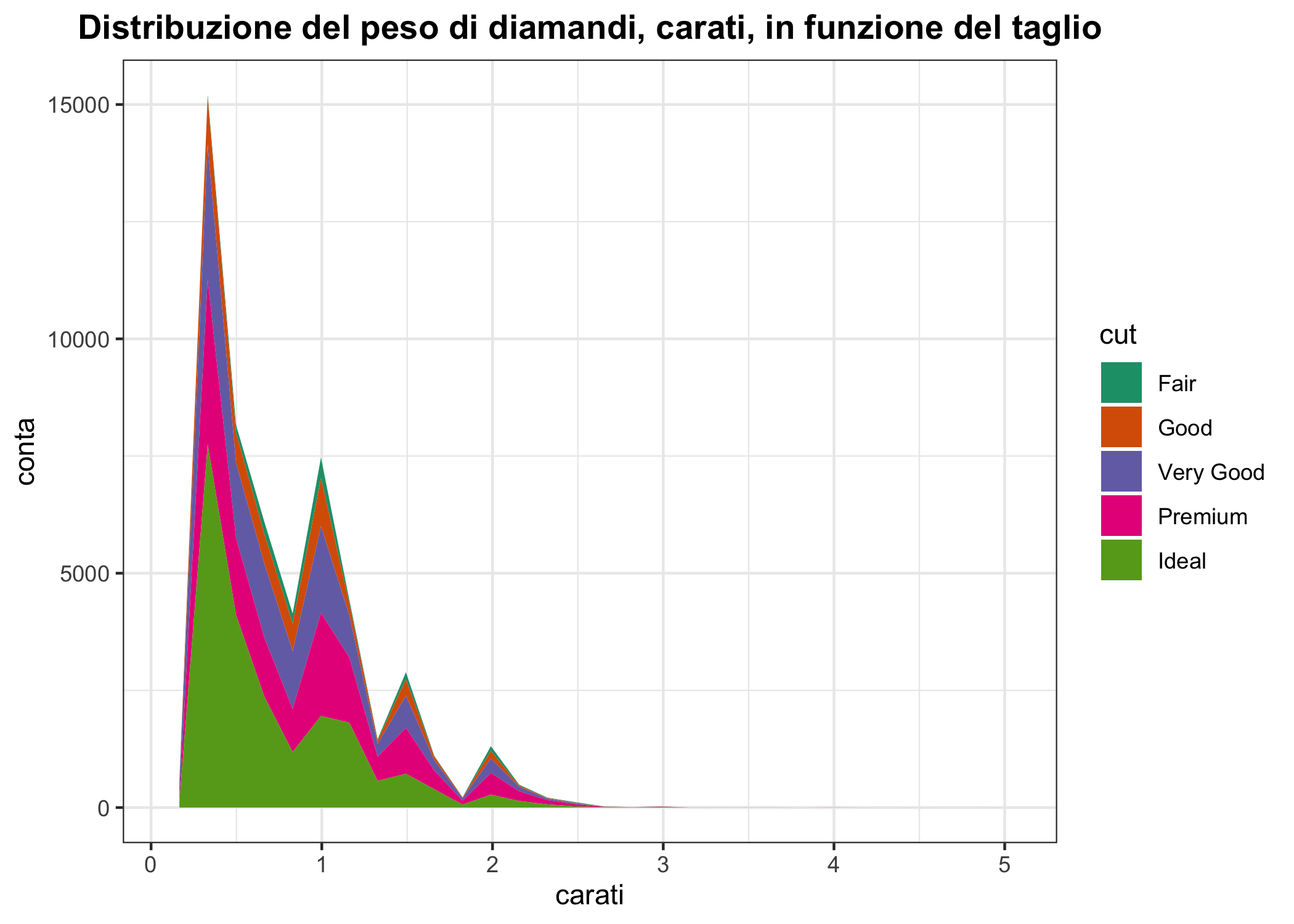
Figura 6.16: Un diagramma ad area impilata della distribuzione del peso di diamanti di taglio diverso in carati.
Un equivalente 2D degli istogrammi sono le heatmap, che usano una gradazione di colore per rappresentare conte o densità diverse. Qui approfitto per mostrare come applicare una facet per taglio e usare una scala logaritmica per le conte. Vale appena la pena di ricordare che le gradazioni di colore non sono il modo migliore per fare confronti quantitativi.
ggplot(diamonds, aes(x= carat, y = price)) +
geom_bin2d(bins = c(20,20)) +
facet_grid(~ cut) +
ggtitle("distribuzione dei diamanti, per prezzo e peso in carati") +
scale_fill_gradientn(colours = heat.colors(10), trans = "log1p",
breaks = scales::trans_breaks("log10", function(x) 10^x)) +
labs(title = "distribuzione dei diamanti, per prezzo e peso in carati",
x = "Prezzo, US$",
y = "Peso, carati") +
theme_bw() +
theme(plot.title = element_text(hjust = 0.5, face = "bold"))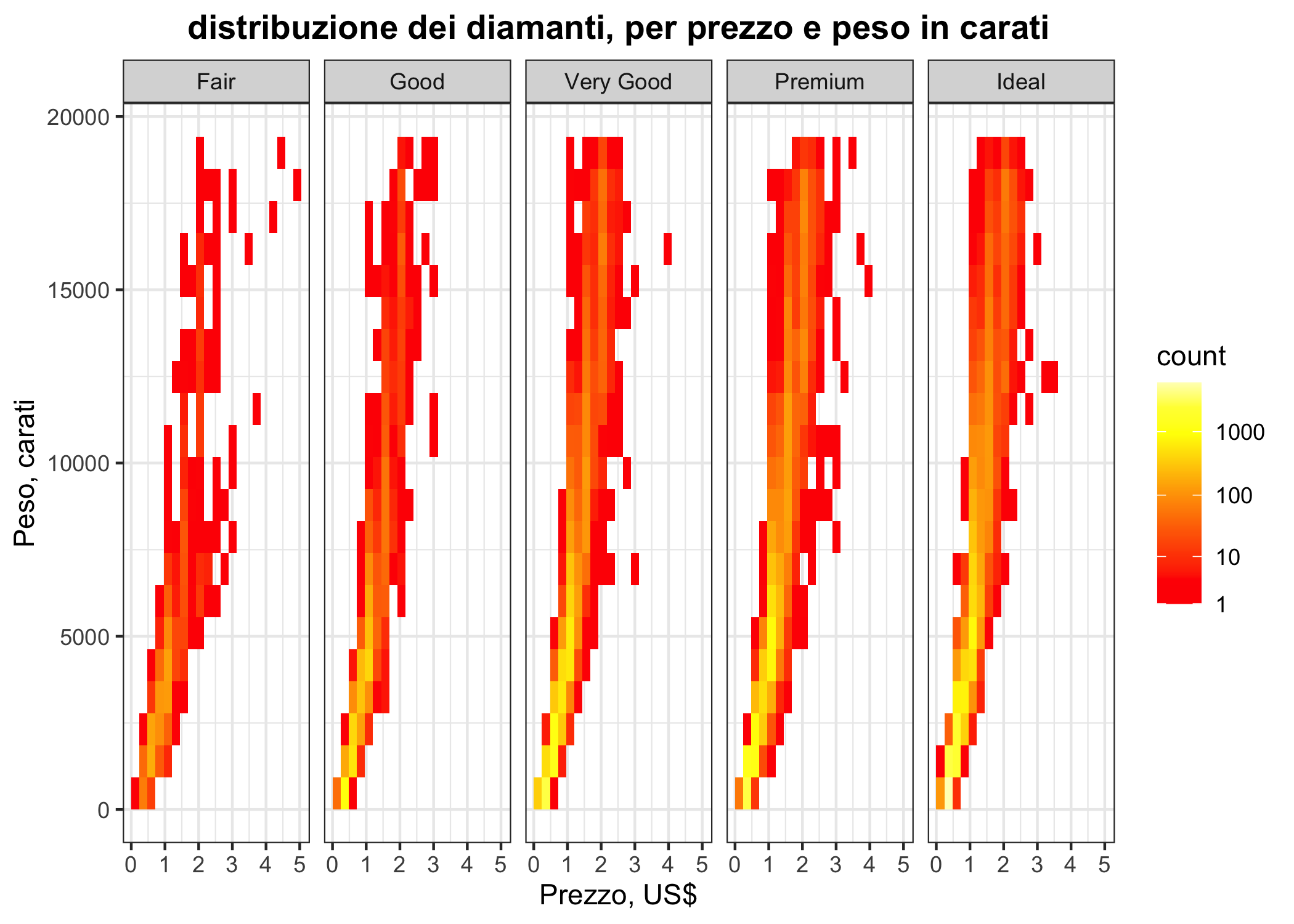
Figura 6.17: Un esempio di heatmap (mappa di calore).
Approssimazioni continue della densità (in una o due dimensioni) possono essere ottenute utilizzando delle stime kernel della densità, con metodi parametrici o non parametrici: si tratta di funzioni che utilizzano la densità locale dei punti per ottenere una linea continua che approssima la densità145. ggplot2 consente di usare diversi kernel; il kernel di default è “gaussian”, ma altre opzioni sono, per esempio “epanechnikov”, “rectangular”, “triangular”. Confronta la figura successiva con l’istogramma o il poligono di frequenza delle figure 6.14 e 6.15.
dfpoly +
geom_density(aes(colour = cut), kernel = "e") +
labs(x = "peso in carati", y = "densità", colour = "taglio") +
scale_colour_brewer(type = "qual", palette = "Dark2") +
theme_bw()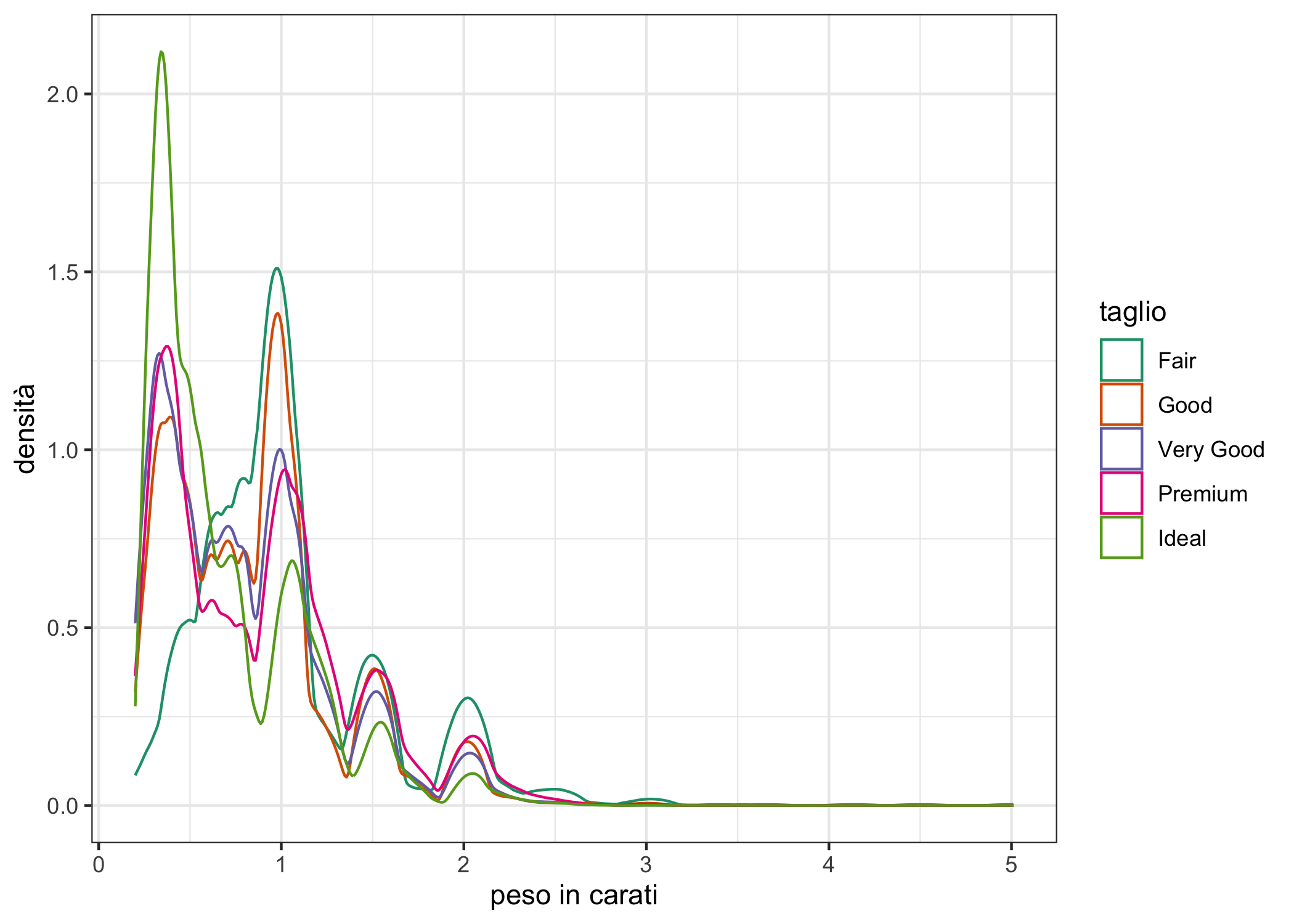
(#fig:densita_continua)Un grafico a desità della dimensione in carati di diamanti, per diamanti di taglio diverso.
Prova in uno script o nella console il codice successivo per ottenere delle rappresentazioni in 2D e pensa a come migliorarle (p.es. cambiando le scale come mostrato negli esempi precedenti). Nota anche come qui ho usato un valore di trasparenza molto basso e una dimensione dei simboli molto piccola: questa pratica può essere conveniente quando ci sono moltissimi punti e si vuole mantenere una sensazione della densità senza rendere il grafico troppo “pesante”.
# un grafico a dispersione con due rappresentazioni della densità:
# dei rug plot sugli assi e un contour plot
# prova a sperimentare con vari valori di n in geom_density_2d
ggplot(dplyr::filter(diamonds, carat<3), aes(x= carat, y = price)) +
geom_point(size = I(0.05), alpha = 0.1) +
geom_rug(sides = "bl", alpha = 0.005) +
geom_density_2d(n = 100, colour = "red") +
labs(x = "peso in carati", y = "densità") +
theme_bw()
# qui escludo i diamanti più grandi che sono pochissimi
ggplot(dplyr::filter(diamonds, carat<1.5, price <5000), aes(x= carat, y = price)) +
geom_density_2d_filled(alpha = 0.5, contour_var = "count") +
scale_x_continuous(limits = c(0,1.5), breaks = seq(0,1.5,0.1),
minor_breaks = seq(0,3, 0.1))+
labs(x = "peso in carati", y = "prezzo, US$") +
theme_bw()
# un'altra possibilità è usare una scala continua
ggplot(dplyr::filter(diamonds, carat<1.5, price <5000), aes(x= carat, y = price)) +
stat_density_2d_filled(geom = "raster",
aes(fill = after_stat(density)),
contour = FALSE,
n=200
) +
scale_fill_viridis_b(direction = -1, option = "C")+
scale_x_continuous(limits = c(0,1.5), breaks = seq(0,1.5,0.1),
minor_breaks = seq(0,3, 0.1))+
labs(x = "peso in carati", y = "prezzo, US$") +
theme_bw()6.8.2 Boxplot.
I boxplot (o più propriamente, box and whiskers plots, che in italiano si traduce grafico a scatole e baffi) e le loro variazioni sono un altro modo per rappresentare la distribuzione delle osservazioni, oltre che per mostrare alcuni utili indicatori non parametrici (la mediana, il range interquartile vedi capitolo 7). Boxplot assolutamente dignitosi possono essere ottenuti usando la funzione boxplot() della grafica di base. La funzione geom_boxplot() fornisce flessibilità addizionale ma ha anche alcune particolarità noiose (richiede sia una variabile x, di solito qualitativa, che una variabile y, quantitativa, quella per la quale interessa analizzare la distribuzione).
survey_dati_completi <- survey %>% tidyr::drop_na()
ggplot(survey_dati_completi, aes(x=Sex, y=Height)) +
geom_boxplot() +
labs(
title = "Altezza in cm di studenti della Univ. Adelaide",
caption = "Venables, W. N. and Ripley, B. D. (2002) Modern Applied Statistics with S-PLUS. Fourth Edition. Springer.",
x = "Sesso",
y = "Altezza, cm") +
scale_x_discrete("Sesso", labels = c("Female" = "Femmine", "Male" = "Maschi")) +
theme(plot.title = element_text(hjust = 0.5))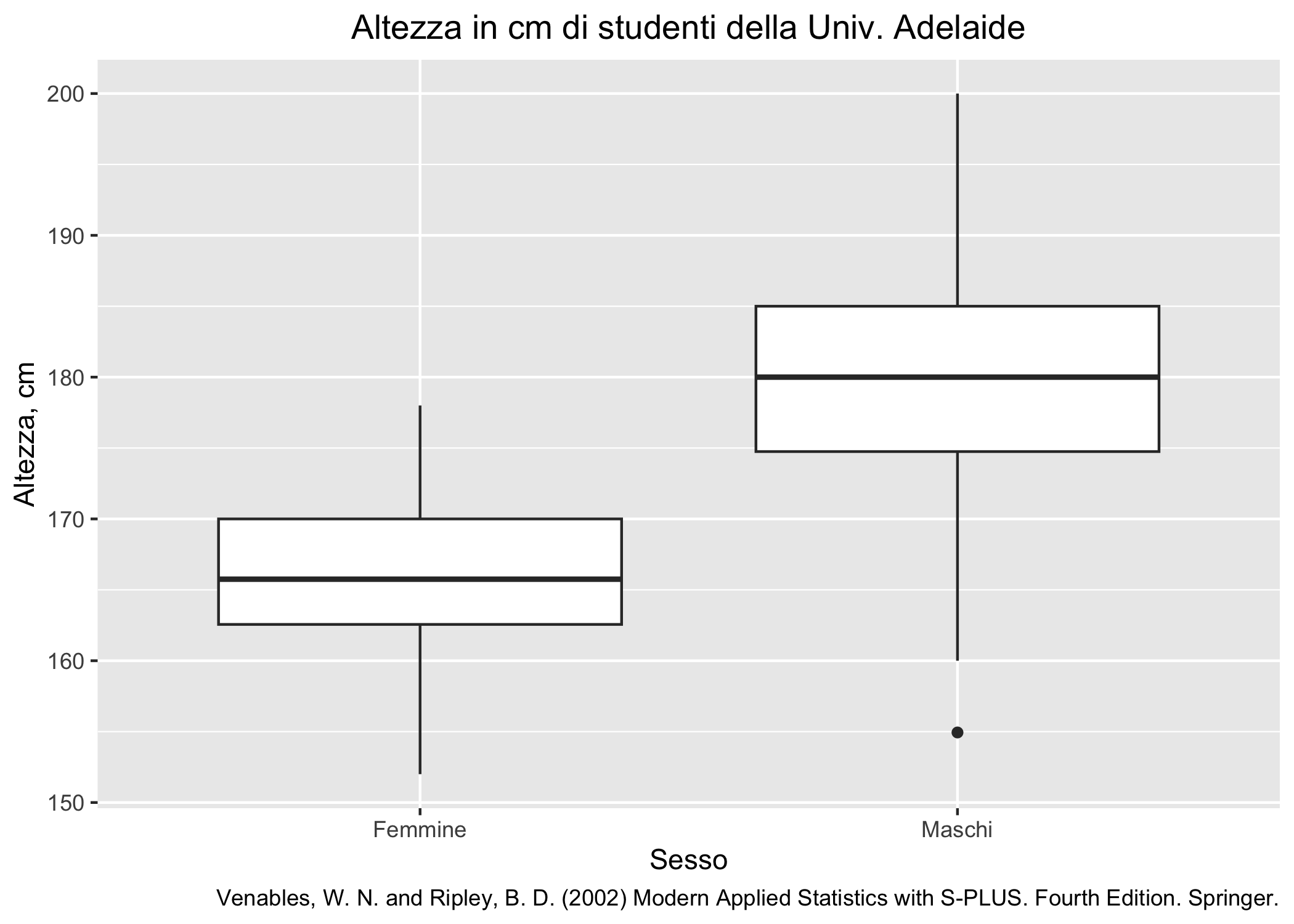
Figura 6.18: Distribuzione dell’altezza di studenti di psicologia dell’Università di Adelaide.
La Figura 6.18 mostra un piccolo esempio creato usando il dataset MASS::survey.
Sono evidenti gli elementi principali del box plot:
la linea spessa orizzontale centrale mostra la mediana delle osservazioni (il secondo quartile,
Q2)il box è delimitato dal 25° e 75° percentile (quantili
Q1eQ3); il range interquartile (IQR) si calcola facilmente comeQ3-Q1e, ovviamente, contiene il 50% delle osservazionii “baffi” (le due linee che partono dal box) sono lunghi al più 1,5*IQR
eventuali osservazioni che eccedono l’intervallo delimitato dai baffi sono rappresentate come cerchi neri pieni e, tendenzialmente, indicano dei valori estremi o outlier
In sostanza, il box plot è ottenuto usando le statistiche che si possono ricavare dalla funzione fivenum().
Vale appena la pena di aggiungere che non ha molto senso usare un box plot con un numero ridotto di osservazioni (diciamo che già 10 possono essere pochine).
Come esercizio mentale prova a pensare quali informazioni puoi ricavare da un box plot (e da questo in particolare) e in che modo ti possono servire a confrontare distribuzioni di un singolo gruppo di osservazioni o di più gruppi di osservazioni.
Prova ora le seguenti opzioni (copiando il codice usato per generare la figura in uno script e cambiando i comandi):
trasponi il grafico aggiungendo
coord_flip()(può essere utile quando le etichette dell’asse delle x sono lunghe, anche se è possibile lavorare su questo aspetto usantotheme())146;prova ad aggiungere l’opzione
geom_boxplot(notch = T)per aggiungere un intervallo di confidenza alla mediana (delimitato dalla zona a clessidra o da “spine” triangolari che si estendono oltre il range interquartileprova ad aggiungere colori dei bordi e riempimenti (in questo caso sono assolutamente inutili, ma potrebbero essere di qualche utilità se si desidera confrontare gruppi diversi delimitati da una seconda variabile qualitativa all’interno dei gruppi delimitati dalla variabile x)
Un box plot può essere arricchito di molti altri elementi:
le singole osservazioni, con una bassa trasparenza, in modo da poter avere una rappresentazione fedele della loro distribuzione
un violin plot (che, in pratica, usa
geom_densityper ottenere una rappresentazione non parametrica della densità), in modo da poter evidenziare eventuali distribuzioni multimodali ed esaltare la presenza di asimmetrie nella distribuzione
ggplot(survey_dati_completi, aes(x=Sex, y=Height)) +
geom_violin() +
geom_boxplot(width = 0.4, colour = "blue", notch = T) +
geom_jitter(colour = I("blue"), alpha = I(0.2), width = 0.2) +
labs(
title = "Altezza in cm di studenti della Univ. Adelaide",
caption = "Venables, W. N. and Ripley, B. D. (2002) Modern Applied Statistics with S-PLUS. Fourth Edition. Springer.",
x = "Sesso",
y = "Altezza, cm") +
scale_x_discrete("Sesso", labels = c("Female" = "Femmine", "Male" = "Maschi")) +
theme(plot.title = element_text(hjust = 0.5))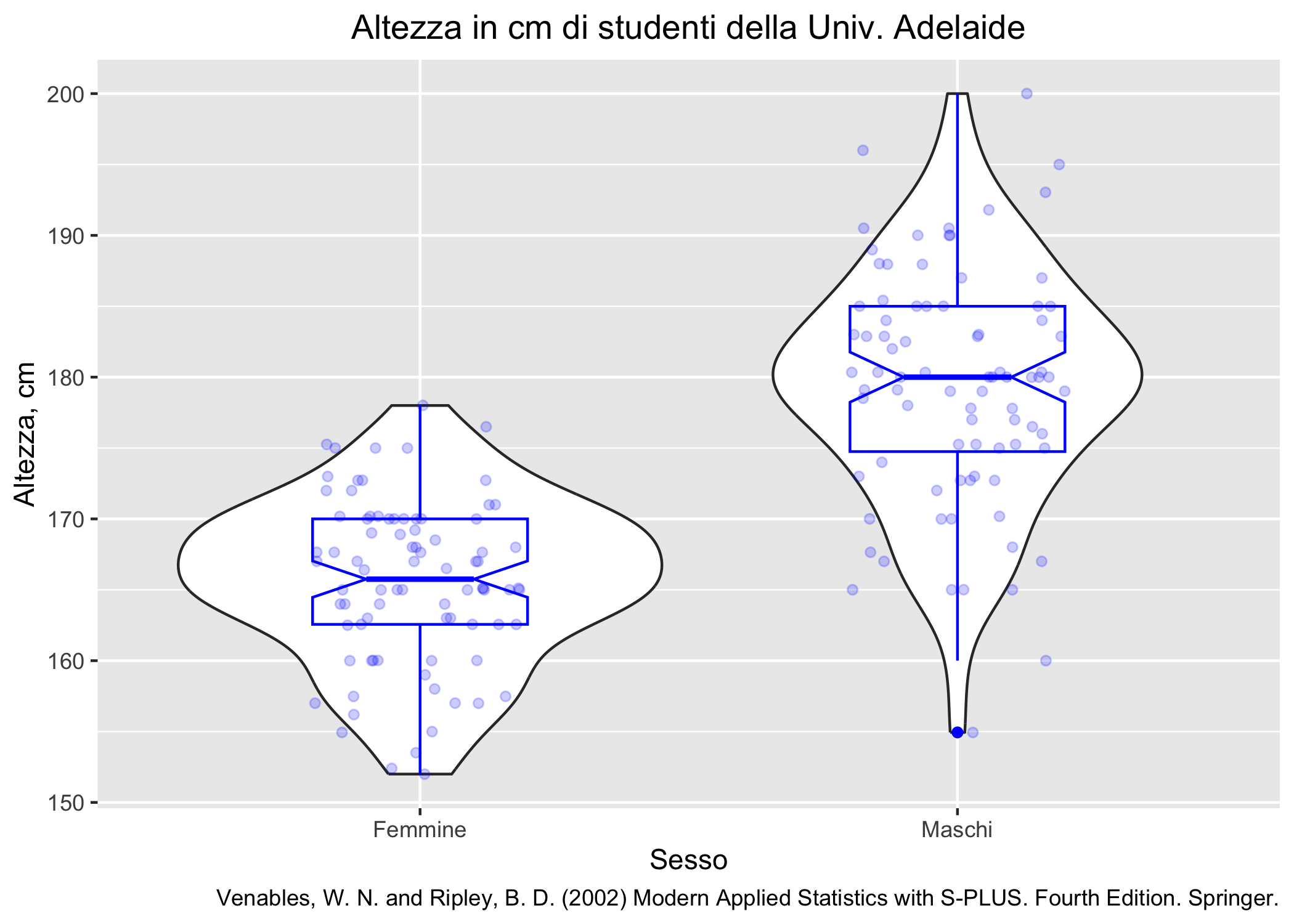
Figura 6.19: Combinazione di box plot, violin plot e jitter plot.
Ulteriori effetti “speciali” possono essere ottenuti con diverse estensioni di ggplot2; ggstatsplot, ggpubr, ggbeeswarm sono solo tre esempi.
Per finire, questa cosa di cambiare le etichette per fare tutto in italiano sta diventando noiosa. Da adesso in poi, visto che hai sicuramente capito come si fa, lascerò tutto in inglese.
6.8.3 Rappresentazioni di indicatori di tendenza centrale e di variabilità.
In diversi casi lo scopo di chi costruisce la visualizzazione dei dati è mostrare qualche indice di tendenza centrale (tipicamente la media o la mediana) accompagnato da un indice di dispersione, che mostri la variabilità o l’incertezza, spesso per più gruppi di osservazioni. ggplot2 offre una varietà di alternative che richiedono in genere una variabile x qualitativa, una variabile y quantitativa e dei valori di ymin e ymax che indicano i limiti inferiore e superiore dell’intervallo che rappresenta incertezza o variabilità. Per questo esempio userò ancora iris, anticipando alcune funzioni per calcolare statistiche riassuntive su gruppi di dati (vedi 7). Approfitto per mostrare l’uso di str_wrap, una funzione del pacchetto stringr, incluso nel tidyverse, utile per mandare a capo del testo molto lungo:
# uso funzioni di `dplyr` per calcolare statistiche per gruppi con `summarise`
# devst è la deviazione standard, IQR il range interquartile e n_oss il
# numero di osservazioni, q25 e q75 il 25° e 75° quantile
data("iris")
iris_stat <- iris %>%
group_by(Species) %>%
dplyr::summarise(mediaPW = mean(Petal.Width),
medianaPW = median(Petal.Width),
devstPW = sd(Petal.Width),
q25 = quantile(Petal.Width, 0.25),
q75 = quantile(Petal.Width, 0.75),
n_oss = n())
# calcolo errore standard e limiti inferiori e superiori dell'intervallo di
# confidenza usando alpha = 0.05
# con gdl = n_oss-1 gradi di libertà
alpha = 0.05
iris_stat <- iris_stat %>%
mutate(errstPW = devstPW/sqrt(n_oss),
gdl = n_oss-1) %>%
mutate(conf_min = mediaPW-qt(alpha/2, df = gdl, lower.tail = F)*errstPW,
conf_max = mediaPW+qt(alpha/2, df = gdl, lower.tail = F)*errstPW
)
# nota come è possibile anche ottenere l'intervallo di confidenza della media
# con t.test() ma occorre estrarre i risultati dalla lista ottenuta con il test
# uso geom_point range con l'intervallo di confidenza
ggplot(iris_stat, aes(x = Species)) +
geom_pointrange(aes(y = mediaPW, ymin = conf_min, ymax = conf_max), size = I(0.2)) +
labs(x = "Specie",
y = str_wrap("Larghezza dei petali, media con intervallo di confidenza, alpha = 0.05", 50))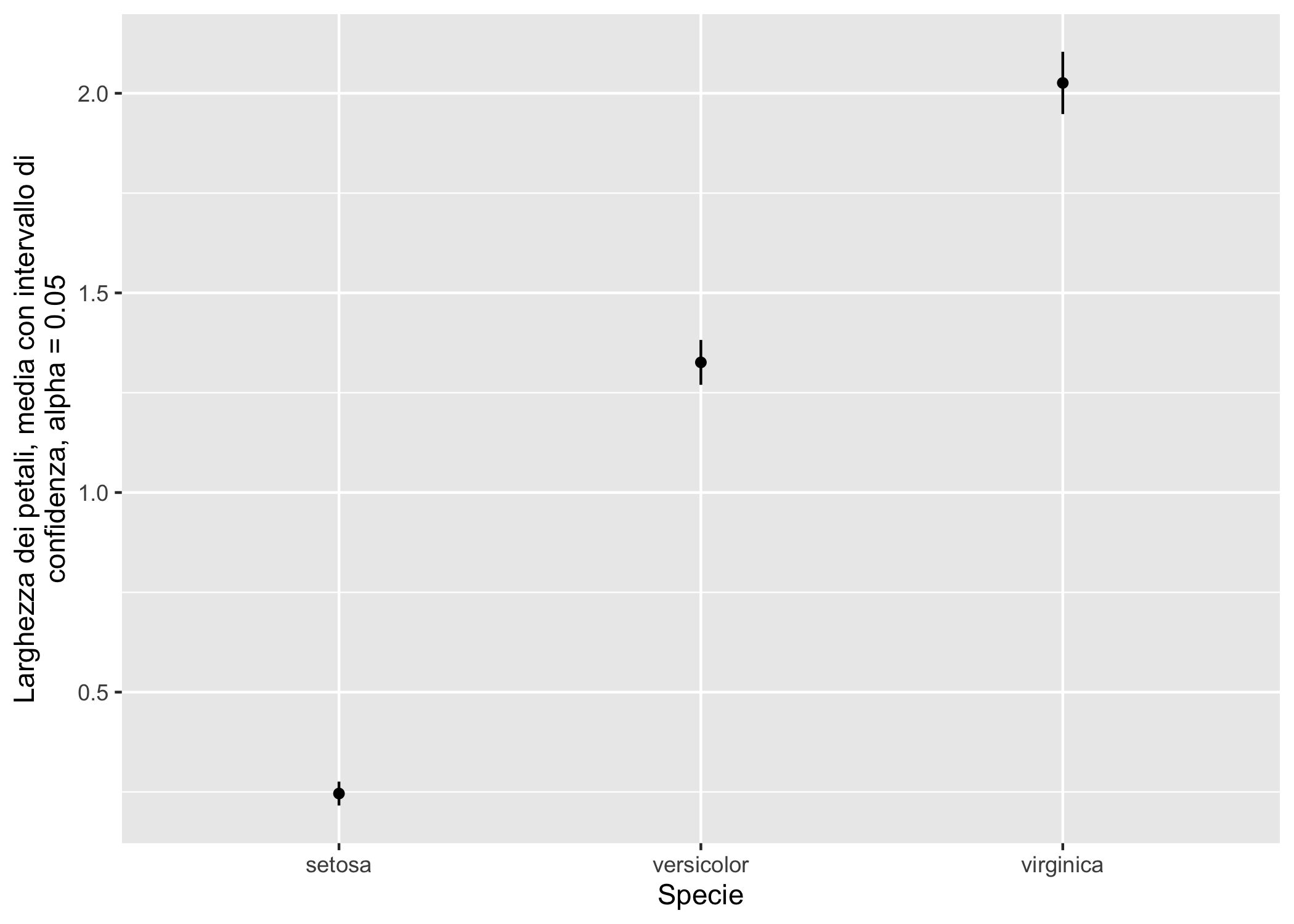
Figura 6.20: Rappresentazioni di indicatori di tendenza centrale e variabilità
Prova ora a sostituire geom_pointrange con geom_crossbar, geom_linerange, geom_errobar (dopo aver dato uno sguardo all’aiuto, naturalmente). Prova anche a sostituire altri valori di y (mediana invece di media, per esempio) o dell’intervallo mostrante la variabilità (media ± deviazione standard, etc.)
Un modo comune per fare la stessa cosa e sprecare molto inchiostro (virtuale) è usare una versione del grafico a barre che non usa conte, ma il valore fornito dalla variabile y, geom_col. Prova questo codice:
# qui uso il colore ma sopprimo la legenda, perché inutile
ggplot(iris_stat, aes(x = Species, y = mediaPW)) +
geom_linerange(aes(ymin = conf_min, ymax = conf_max)) +
geom_col(aes(fill = Species), alpha = 0.5, show.legend = F) +
labs(x = "Specie",
y = str_wrap("Larghezza dei petali, media con intervallo di confidenza, alpha = 0.05", 50))6.8.4 Grafici a dispersione.
I grafici a dispersione (scatterplot in inglese) sono il cavallo da tiro della visualizzazione scientifica dei dati. Sono usati principalmente per mostrare le relazioni fra due variabili continue. Variabili qualitative possono essere attribuite a vari elementi del grafico, come forme, colori (di bordo o riempimento), tipi di linea, facets. Altre variabili quantitative possono essere attribuite a colori e dimensioni (inclusi gli spessori delle linee). Linee di tendenza parametriche o non parametriche possono essere aggiunte con geom_smooth().
Per gli esempi userò alcuni dei data set già utilizzati in questo capitolo, ma potresti provare a usare dati dal pacchetto gapminder o uno dei numerosi data set di R o dei pacchetti.
In ggplot2 il geoma che genera grafici a dispersione è geom_point(). Cominciamo con un esempio semplice semplice usando il classico data set Iris. Qui viene mostrata la relazione fra lunghezza e larghezza dei sepali per tre specie di Iris. Nota l’uso della pipe, %>%, un’operatore creato dal pacchetto magrittr che viene caricato con il tidyverse, per passare i dati alla funzione ggplot() .
irisggplot <- iris %>%
ggplot(aes(x=Sepal.Length, y=Sepal.Width, shape = Species, colour = Species)) +
geom_point()
irisggplot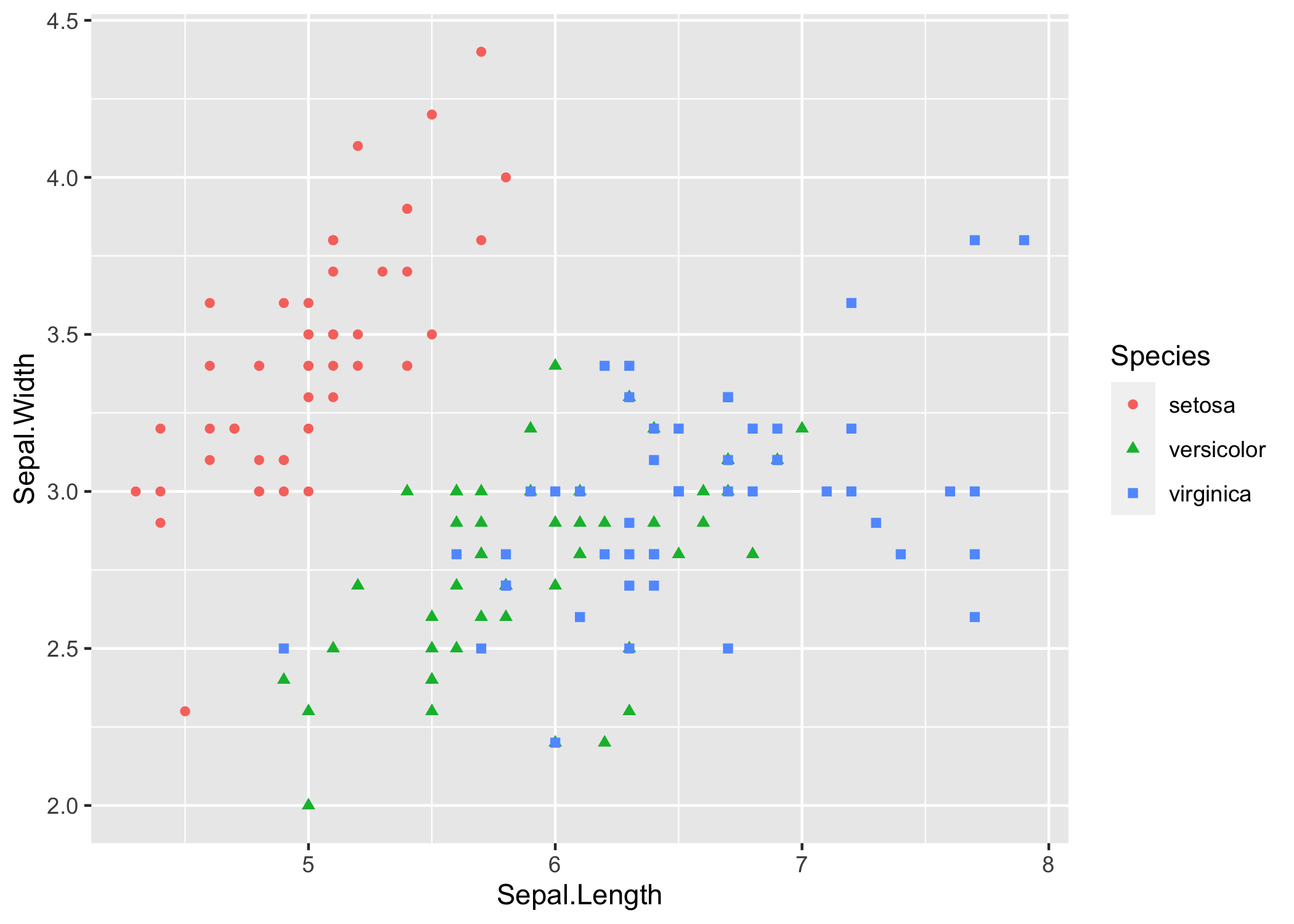
Figura 6.21: Un semplice grafico a dispersione
Semplice e senza fronzoli, no? Prova a pensare come potresti abbellire questo grafico usando i comandi presentati nelle sezioni precedenti. Prova anche a pensare come potresti rendere più evidenti (ricordati che una rappresentazione grafica di dati scientifici racconta una storia) alcuni aspetti biologicamente interessanti:
la divisione in gruppi
la relazione fra le due variabili
Cominciamo ad aggiungere cose: prova questo codice (devi aver fatto girare quello di prima, se no non funziona: perché?):
# un rugplot
irisggplot + geom_rug(sides = "tr")
# uno smoother non parametrico diverso per ciascuno dei gruppi
irisggplot +
geom_rug(sides = "tr") +
geom_smooth()
geom_smooth()è una delle funzioni più utili di ggplot2 quando si voglia evidenziare il trend dei dati. Ti consiglio vivamente di approfondire leggendo l’aiuto e studiando gli esempi.
Qui ripropongo lo più o meno lo stesso codice aggiungendo un ulteriore strato con una regressione lineare e rimuovendo gli intervalli di confidenza e il rug plot:
irisggplot +
geom_smooth(se = F, linewidth = I(0.5)) +
geom_smooth(method = "lm", formula = y ~ x, se = F, linetype = I(2), linewidth = I(0.5))Anche qui: prova ad interpretare il grafico: in che cosa questa rappresentazione dei dati migliora la tua comprensione del fenomeno biologico? Per esempio:
i gruppi corrispondenti alle diverse specie sono ben separati?
esiste una relazione fra le due variabili? É credibile che si tratti di una relazione lineare (anche se quest’ipotesi potrebbe essere dimostrata in maniera più efficace con un test inferenziale)
Bene, ora proviamo a fare le cose per bene: aggiungo anche una rappresentazione della densità parametrica, le ellissi di confidenza.
irisggplot +
geom_smooth(se = F, linewidth = I(0.5)) +
geom_smooth(method = "lm", formula = y ~ x, se = F, linetype = I(2),
linewidth = I(0.5)) +
stat_ellipse(
type = "t",
level = 0.95,
linewidth = I(0.5)
)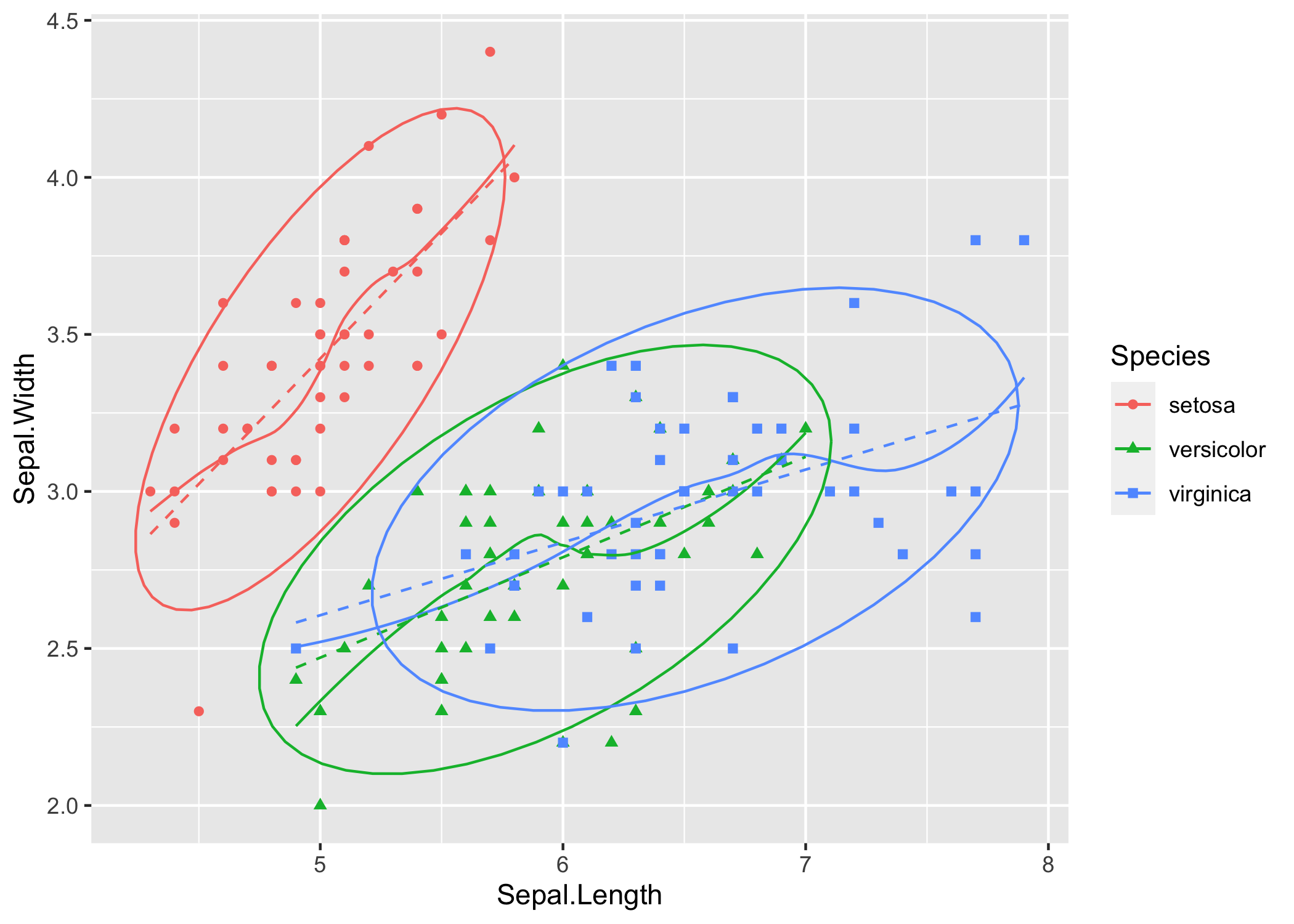
Figura 6.22: Un grafico a dispersione con smoother nn parametrico (loess) linee di regressione e ellissi di confidenza
I parametri di default di stat_ellipse generano l’ellisse usando una distribuzione t di Student bivariata; è possibile usare type = "norm" per ottenere una distribuzione bivariata normale. C’è un po’ di dibattito sul fatto che il metodo scelto da ggplot2 generi effettivamente un’ellisse di confidenza. In ogni caso le cose che dovresti guardare sono:
la dimensione dell’ellisse è in relazione con la variabilità dei dati (varianza della media o del campione); guardando la dimensione relativa ai due assi è possibile vedere quale delle due variabili ha una varianza maggiore
l’inclinazione dell’ellisse è in relazione con la covarianza o la correlazione fra le variabili (se l’asse maggiore è molto inclinato la correlazione o la covarianza sono maggiori; se l’ellisse si approssima ad un cerchio le due variabili non sono correlate)
Ora cambiamo data set per dimostrare alcune altri aspetti interessanti dei grafici a dispersione. ggplot2::mpg è un buon punto di partenza per la combinazione di variabili qualitative e quantitative. Userò una versione filtrata del data set perché, come richiamato nella sezione 6.2 non è opportuno usare troppe combinazioni diverse di colori e simboli. Cominciamo per dimostrare come una terza variabile quantitativa possa essere attribuita al colore (deve essere una variabile continua!) o alla dimensione del simbolo). In questo caso forzeremo un po’ la scelta dei simboli. Ah dimenticavo, R ti permette di usare 25 simboli grafici diversi, oltre alle lettere dell’alfabeto: se vuoi una lista cerca sul web o, meglio ancora, usa questi comandi
install.packages("ggpubr") # necessario solo se non è già presente nella libreria
library(ggpubr)
ggpubr::show_point_shapes()Nota anche qui l’uso della funzione filter del pacchetto dplyr per selezionare in modo facile solo una parte delle osservazioni del data frame (le 6 classi di veicoli più numerose). Ricorda anche come gli estetici possono essere passati nel primo strato (quello con ggplot), e in questo caso sono ereditati dai geomi successivi, oppure direttamente nei geomi. Visto che ci siamo, mostro come si possa cambiare la posizione della legenda e il numero di colonne di alcuni elementi della legenda.
Nel primo grafico in cui la dimensione del simbolo è in funzione della cilindrata e il colore in funzione del tipo di carburante, una variabile qualitativa; cambio i simboli con scale_shape_manual(), creando un vettore con nomi con le forme che voglio usare (cerchi, triangoli, quadrati, rombi).
mpg_ridotto <- mpg %>%
dplyr::filter(class %in% c("compact", "midsize", "subcompact", "suv"))
mpg_layer_base <- ggplot(mpg_ridotto, mapping = aes(x=cty, y = hwy))
my_shapes <- c("compact" = 16, "midsize" = 17, "subcompact" = 15, "suv" = 18)
mpg_cty_hwy_displ <- mpg_layer_base +
geom_point(aes(shape = class, size = displ, colour = fl)) +
scale_shape_manual(values = my_shapes) +
scale_colour_brewer(type = "qual", palette = "Paired") +
labs(title = "geom_point") +
guides(size = guide_legend(ncol = 2),
colour = guide_legend(ncol = 2)) +
theme_bw() +
theme(plot.title = element_text(hjust = 0.5),
legend.position = "right")
mpg_cty_hwy_displ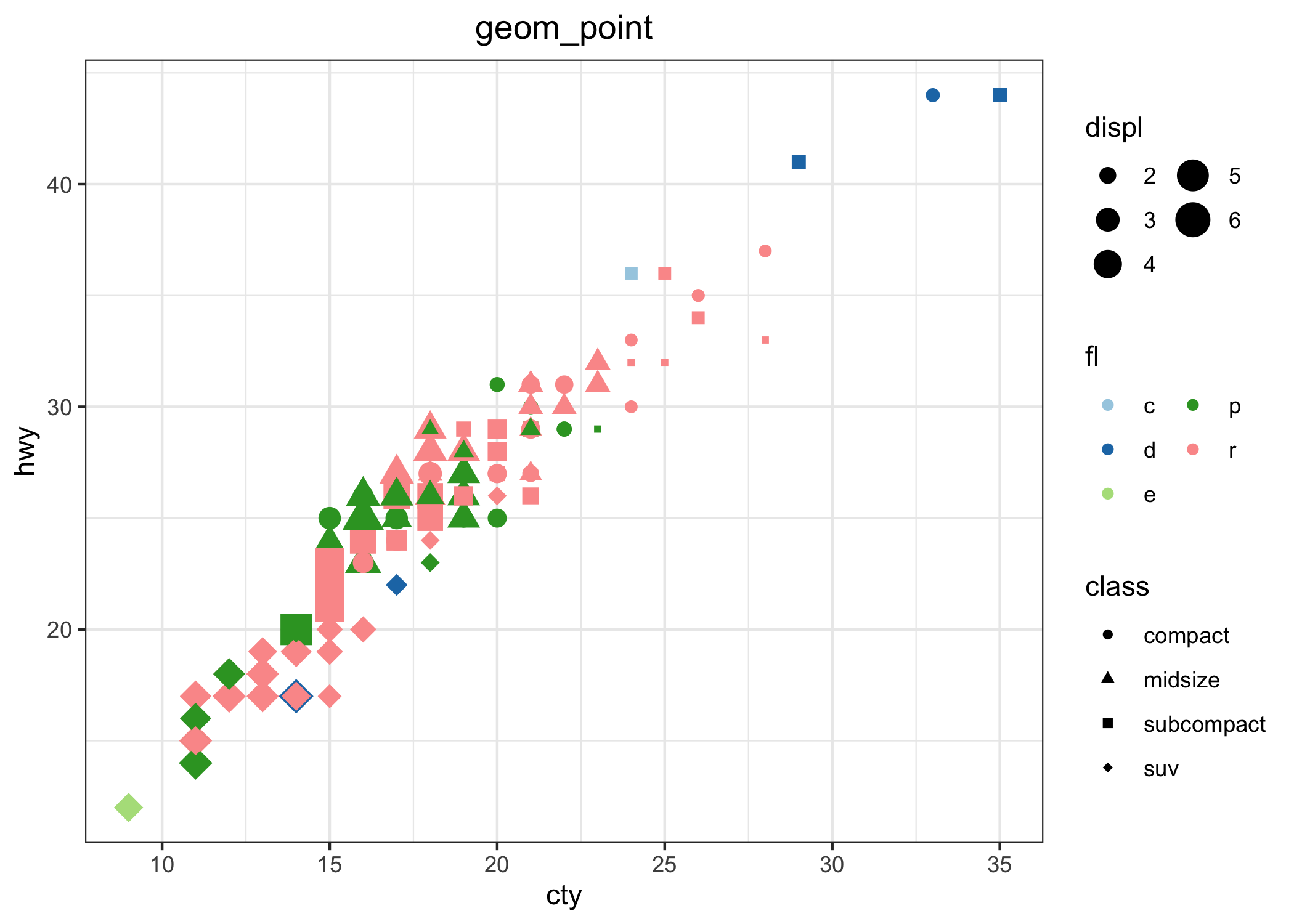
Figura 6.23: Un bubble plot
Semplice, no? Questo grafico si chiama bubble plot ed è molto utilizzato, anche se la nostra capacità di comparare aree non è proprio il massimo. La relazione fra il consumo di carburante in città e in autostrada è praticamente lineare. Sapresti come aggiungere un’unica linea di regressione?
Nota anche come ci sia un problema di “overplotting” (molti punti si sovrappongono), per risolvere il quale uso geom_jitter(), che aggiunge un piccolo spostamento casuale sulle x e sulle y (rischiando ovviamente di perdere un po’ di precisione). Infine, uso le scale del pacchetto viridis che forniscono gradienti ottimizzati per il daltonismo.
mpg_cty_hwy_displ_2 <- mpg_layer_base +
geom_jitter(aes(shape = class, colour = displ)) +
scale_shape_manual(values = my_shapes) +
scale_colour_viridis(option = "B") +
labs(title = "geom_jitter") +
theme_bw() +
theme(plot.title = element_text(hjust = 0.5),
legend.position = "bottom")
mpg_cty_hwy_displ_2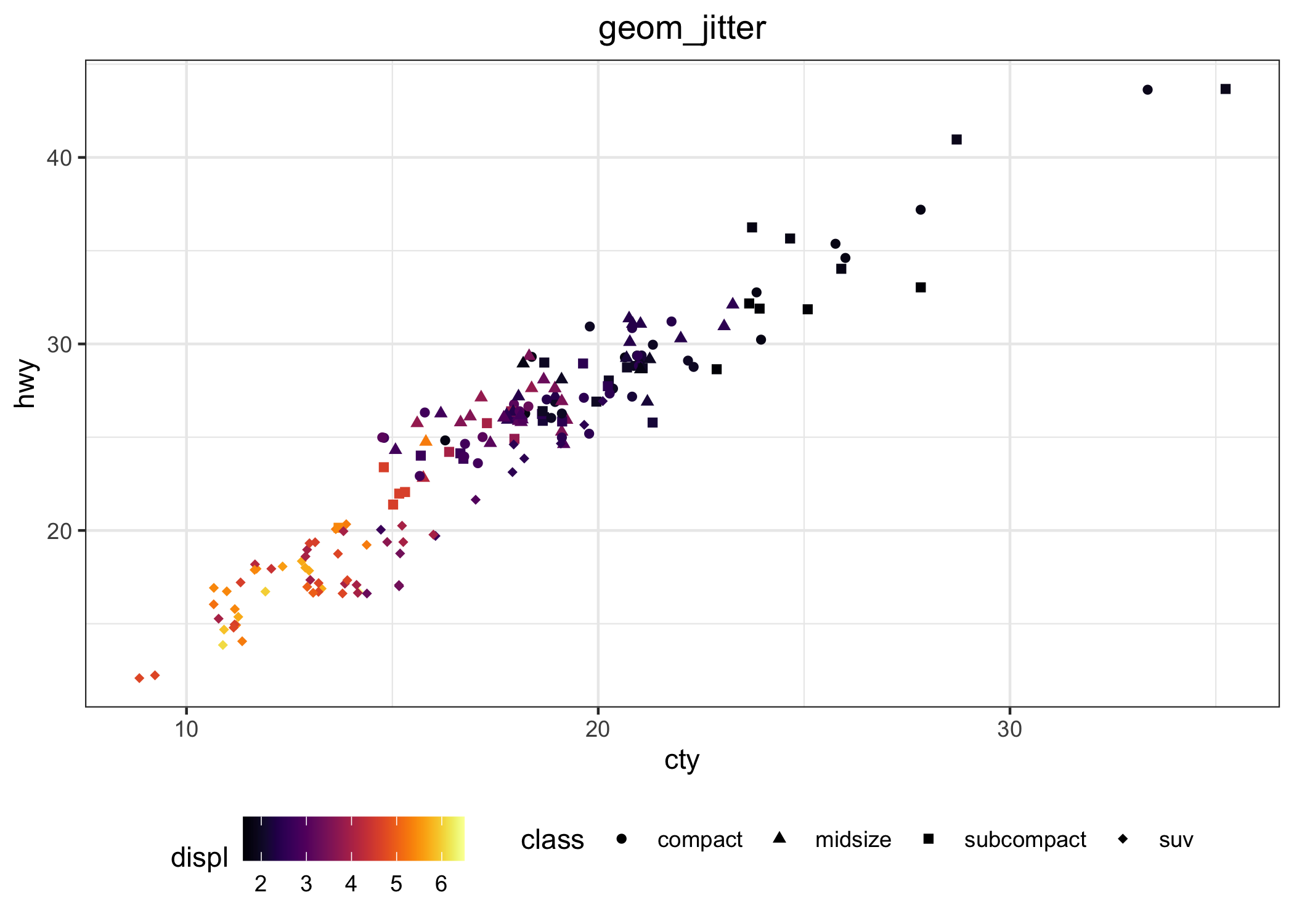 ***
***
Beh, nel frattempo ti starai chiedendo: e i grafici a dispersione in 3 dimensioni? Dimenticali, per molte ragioni è difficile estrarre informazioni quantitative affidabili da un grafico in 3D, specialmente se aggiungi colori, gradazioni, dimensioni, superfici etc. Ovviamente, se proprio insisti a volerli realizzare puoi cercare in una delle risorse che ti propongo nella sezione 6.10.
Proviamo ora a spostare la variabile class sulle facet e usare il numero di cilindri per la forma dei simboli: prova a chiederti perché devo trasformare questa variabile in un fattore.
mpg_cty_hwy_displ_3 <- mpg_layer_base +
facet_wrap(~class) +
geom_jitter(aes(colour = displ, shape = as.factor(cyl))) +
scale_colour_viridis(option = "B") +
labs(title = "geom_jitter e facets", shape = "cyl") +
scale_shape_manual(values = c(16,17,15,18)) +
theme(plot.title = element_text(hjust = 0.5))
mpg_cty_hwy_displ_3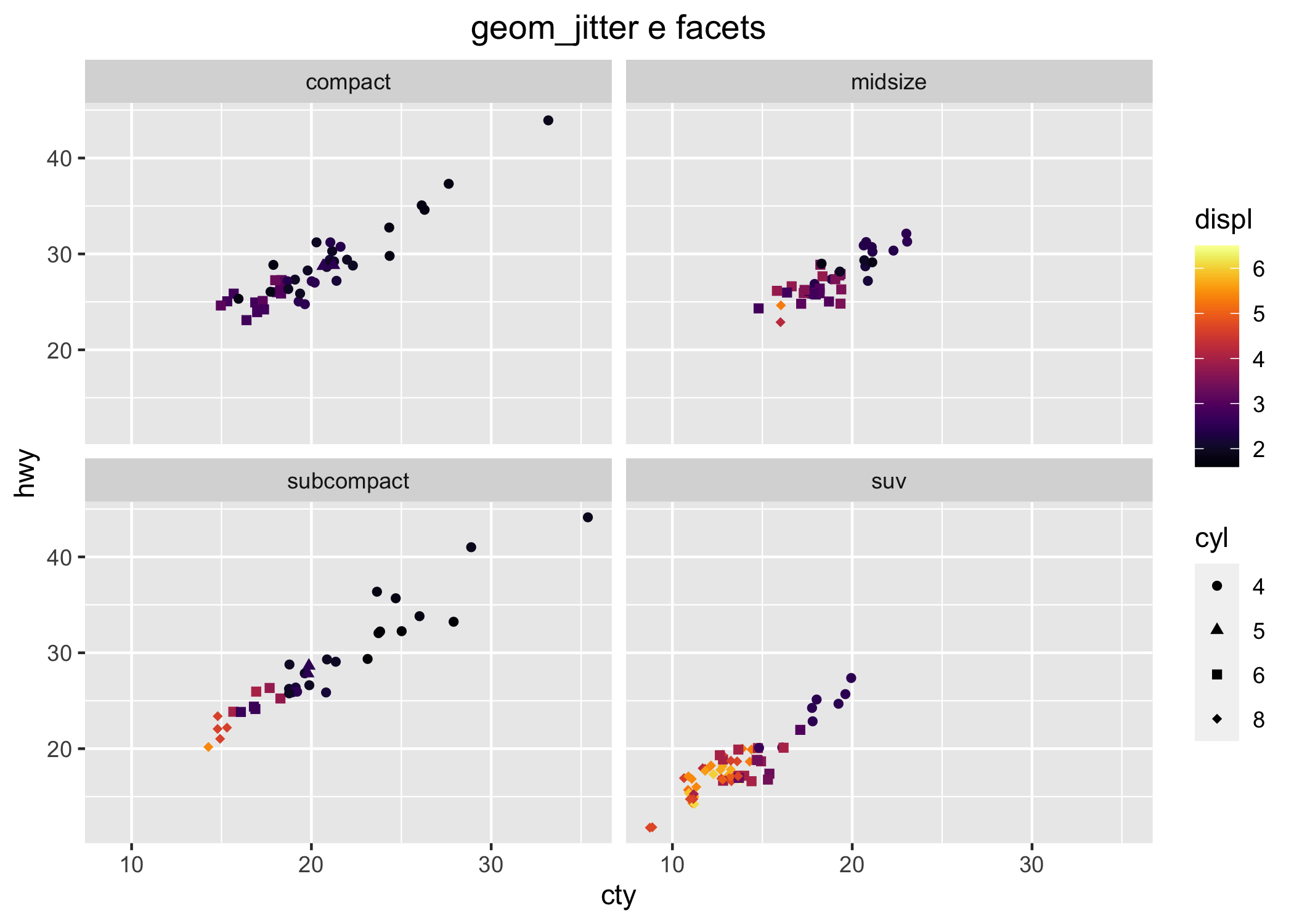
Figura 6.24: Grafico a dispersione con facets.
Insomma, ci sarebbe ancora molto da vedere, soprattutto in termini di geomi e annotazioni ma credo sia più semplilce e meno stancante mostrare nuovi esempi man mano che andiamo avanti. Incidentalmente, prova ad esplorare geom_text e geom_label, due interessanti alternative per etichettare i punti in un grafico a dispersione (che purtroppo possono rendere i grafici piuttosto ingarbugliati).
Se hai fretta puoi cercare in una delle molte eccellenti risorse che ti propongo nella sezione 6.10.
6.8.5 Personalizzare i grafici con ggplot2.
ggplot2 e le sue estensioni (vedi dopo) permettono un livello di personalizzazione veramente eccezionale dei grafici. Il modo più semplice per cambiare in gruppo una serie di elementi (assi, sfondo, etc.), è usare i temi. Prova per esempio a personalizzare l’ultimo grafico variando i temi:
mpg_cty_hwy_displ_3 + theme_bw()
mpg_cty_hwy_displ_3 + theme_classic()
mpg_cty_hwy_displ_3 + theme_dark()
mpg_cty_hwy_displ_3 + theme_light()
mpg_cty_hwy_displ_3 + theme_minimal()Altri temi sono resi disponibili dall’estensione ggthemes. Inoltre, il comando theme() permette, come hai già visto, di cambiare praticamente tutti gli elementi (inclusi, fra le altre cose, orientazione e font delle etichette degli assi).
I pacchetti addizionali come scales (che viene caricato con ggplot2) permettono di personalizzare in molti modi le scale come visto in alcuni esempi, e il comando annotate() permette di aggiungere uno strato con annotazioni (testo, segmenti, persino geomi). Insomma, tanta roba e qui non abbiamo spazio-tempo e, forse, non ne vale la pena: potrai sempre cercare fra le risorse che ti propongo (6.10) o semplicemente sfruttare una delle strategie per cercare aiuto in rete proposte nel 3.
6.8.6 Estensioni per ggplot2.
Molti altri pacchetti forniscono funzionalità aggiuntive a ggplot2 o permettono di usare come input oggetti diversi dai dataframe (come alcune classi di oggetti prodotti da analisi statistiche). Una lista completa delle estenisoni è disponbile qui. Alcune estensioni sono state citate nei paragrafi precedenti.
6.8.7 Veloce veloce: qplot()
Il comando qplot forniva, nelle versioni di ggplot2 precedenti alla 3.4, un’interfaccia rapida per la produzione di grafici in un solo comando. Nonostante questo comando sia deprecato (cioé non verrà più sviluppato a partire da questa versione) è ancora attivo, anche se genera degli avvisi (warning). La struttura generica dei comandi qplot è:
qplot(x, y, ..., data, facets,margins, geom, xlim, ylim, log, main, xlab, ylab, asp)Molti di questi parametri hanno dei default e, tecnicamente, qplot è in grado di proporre il geom più adatto ad una data tipologia di dati, in base alla presenza/assenza delle variabili x e y e alla loro natura (qualitativa o quantitativa).
Prova ad eseguire, nella console o in uno script, questi comandi
# uno scatterplot (generato in automatico perché x e y sono quantitative)
data(mpg)
qplot(x = displ, y = hwy, data = mpg)
# con qualche personalizzazione in più
qplot(x = displ, y = hwy, shape = factor(cyl), data = mpg)
# un barplot (il default per una sola variabile x qualitativa)
qplot(x = class, data = mpg)
# un istogramma (il default per una sola variabile x quantitativa)
qplot(x = displ, data = mpg)
# diventa un density plot se si indica il geoma
qplot(x = displ, data = mpg, geom = "density")
# con facets
qplot(x = displ, data = mpg, geom = "density", facets = ~factor(cyl))
# altri estetici e etichette e titoli,
qplot(displ, hwy, data = mpg, colour = factor(cyl),
main = "cilindrata e consumo in autostrada",
xlab = "cilindrata",
ylab = "miglia per gallone in autostrada")
# un bubble plot
qplot(displ, hwy, data = mpg, colour = factor(cyl), size = cty)
# una combinazione di grafici
qplot(class, hwy, data = mpg, geom = c("jitter", "boxplot"), alpha = I(0.6))
qplot(displ, hwy, data = mpg, geom = c("point", "smooth"))
Prova ad esplorare tu stess* con altre opzioni e combinazioni o a realizzare i grafici ottenuti nei paragrafi precedenti con ggplot. Ti renderai conto che qplot permette di ottenere scrivendo molto meno codice dei grafici accettabili per la fase esplorativa, ma che la flessibilità di ggplot è molto superiore.
6.9 La grafica di base in R: un salvagente?
La grafica di base di R usa un numero limitato di funzioni per costruire visualizzazioni di dati. Esempi di queste funzioni sono:
barplot(), costruisce barplotboxplot(), costruisce boxplothistogram(), costruisce istogrammiplot(), costruisce grafici a dispersione (e molto altro)pairs(), costruisce matrici di grafici a dispersionemosaicplot()grafici a mosaico
Mentre i nomi delle funzioni possono essere intuitivi, i loro parametri sono molto difficili da memorizzare, anche se, come per ggplot2, consentono una personalizzazione molto fine della visualizzazione. Inoltre, realizzare grafici con diversi gruppi è spesso laborioso, perché occorre sovrapporre grafici diversi che usano ciascuno i punti del gruppo da plottare. Mostro qui solo due esempi. La figura 6.25 è un diagramma a barre che mostra i dati del data set Arthritis. E’ l’equivalente della Figura 6.10:
# bisogna prima ricavare la tabella delle conte
Arthritis_tabulazione <- xtabs( ~ Improved + Treatment, data = Arthritis)
# poi lo strato ocn il barplot
barplot(Arthritis_tabulazione, col = rainbow(3), ylim = c(0,50))
# poi la legenda
legend(x = "top", legend = levels(Arthritis$Improved), pch = 15, col = rainbow(3), ncol = 3)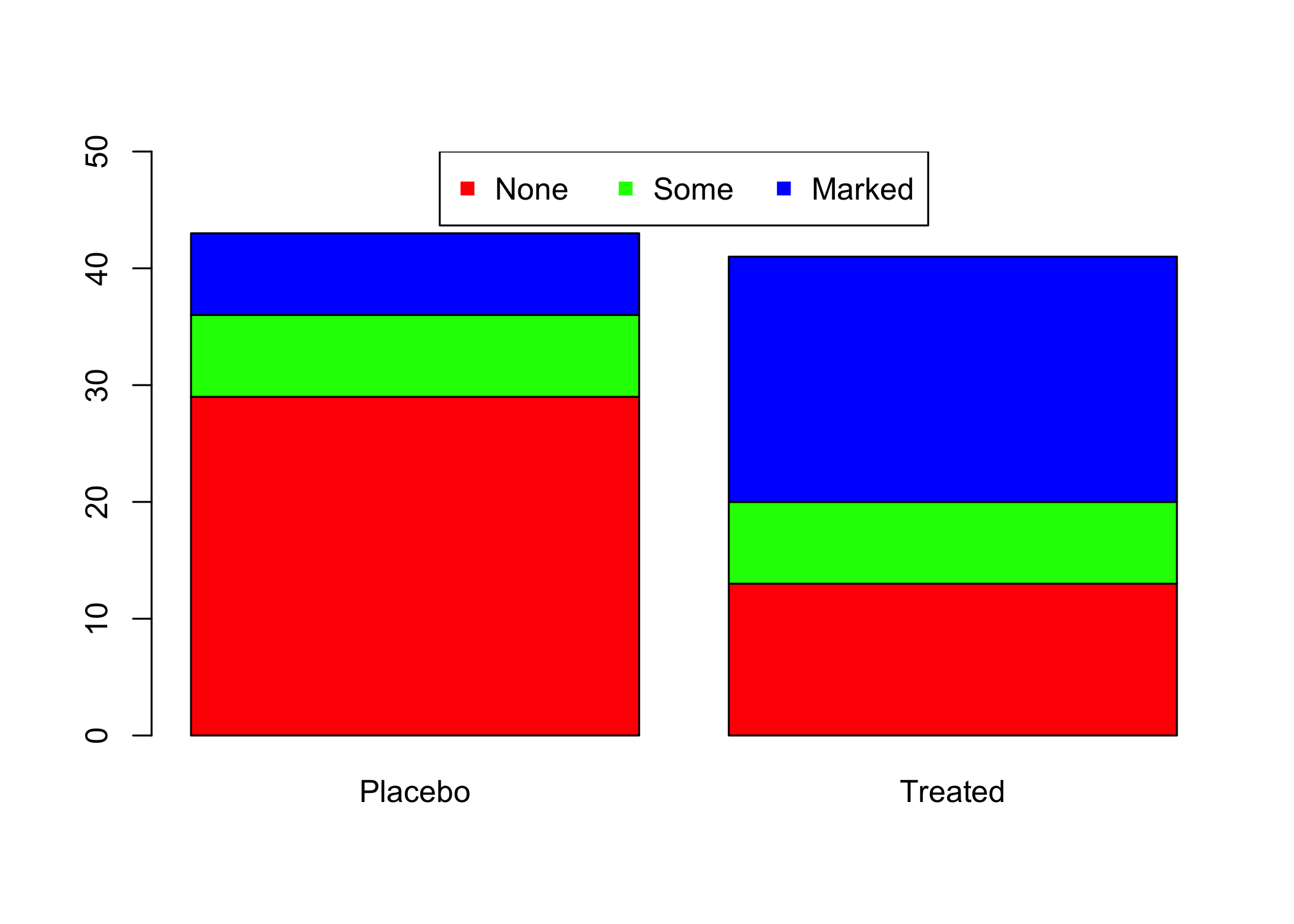
Figura 6.25: Un grafico a barre realizzato con la grafica di base
La figura 6.26 è invece analoga alla figura 6.22. Nota come qui i diversi gruppi sono aggiunti uno dopo l’altro allo strato di base:
# puoi farti un'idea del range ideale con
# range(iris$Sepal.Length)
# range(iris$Sepal.Width)
plot(Sepal.Length ~ Sepal.Width, data = subset(iris, Species == "setosa"),
pch = 16, col = "red", las = 1,
xlab = "larghezza dei sepali", ylab = "lunghezza dei sepali",
main = "relazione fra larghezza e lunghezza dei sepali in tre specie di Iris",
xlim = c(2,5), ylim = c(4,8))
abline(lm(Sepal.Length ~ Sepal.Width, data = subset(iris, Species == "setosa")),
col = "red", lty = 1)
points(Sepal.Length ~ Sepal.Width, data = subset(iris, Species == "versicolor"),
pch = 17, col = "blue", xlab="", ylab="", las = 1)
abline(lm(Sepal.Length ~ Sepal.Width, data = subset(iris, Species == "versicolor")),
col = "blue", lty = 2)
points(Sepal.Length ~ Sepal.Width, data = subset(iris, Species == "virginica"),
pch = 15, col = "cyan", xlab="", ylab="", las = 1)
abline(lm(Sepal.Length ~ Sepal.Width, data = subset(iris, Species == "virginica")),
col = "cyan", lty = 3)
legend(x = "bottomright",
legend = levels(iris$Species), pch = c(16,17,15), col = c("red", "blue", "cyan"))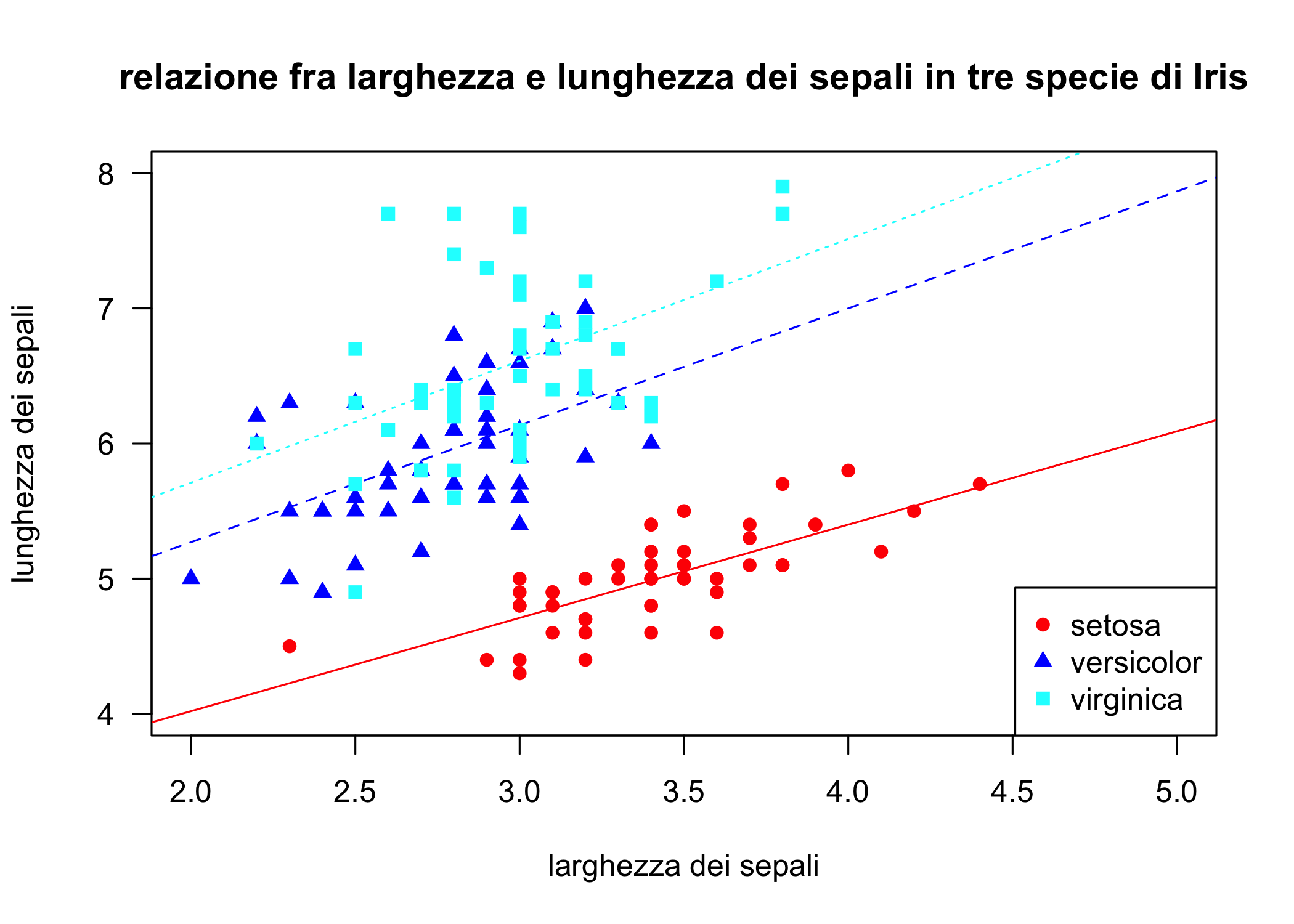
Figura 6.26: Un grafico a dispersione realizzato con la grafica di base
Perché fare tutta questa fatica per un risultato francamente bruttino? Beh, in molti casi i comandi della grafica di base di R consentono di ottenere delle visualizzazioni decenti con poco codice. Poi, e soprattutto, plot() è una funzione generica e serve a ottenere grafici specializzati da molti oggetti ottenuti da analisi statistiche. Prova il codice successivo, che permette di ottenere una in automatico i grafici che rappresentano i diagnostici dell’analisi della varianza per la lunghezza dei petali in iris:
par(mfrow=c(2,2))
plot(aov(Petal.Length ~ Species, data = iris))
par(opar)Inoltre, molti pacchetti hanno funzioni che restituiscono grafici costruiti con la grafica di base (o, se è per questo, con lattice) e può tornare utile saperne qualcosina per poterli personalizzare al meglio (anche se, pian pianino, le estensioni di ggplot2 stanno rendendo più semplice il lavoro di rappresentare graficamente oggetti anche complessi derivanti da analisi statistiche). Comunque, vedremo diversi esempi più avanti.
6.10 Altre risorse.
Il materiale in questo capitolo è presentato in molte delle risorse citate nel capitolo 4. In Italiano non c’è granché, se non la wiki Ricerca sociale con R.
6.10.1 Risorse in inglese.
Di risorse sulla grafica (scientifica e per la data science) con R è pieno il mondo. In effetti, c’è solo da scegliere, e non è per niente facile. Riporto qui una selezione delle risorse che io ho trovato più utili. Un post interessante e visualmente molto ben organizzato sulla grammatica della grafica è qui.
Documenti e pagine web.
Libri: provate questi
come sempre R for data science fornisce esempi ed esercizi interessanti
i soliti libri introduttivi alla statistica e grafica con R (YaRrr!, Just enough R, etc.)
un bel manuale dedicato a ggplot2
un libro molto completo sulla visualizzazione dei dati
un libro di ricette per la grafica con R di R. Kabacoff: può essere un po’ noioso ma è ricchissmo di esempi e la sua organizzazione per tipologie di dati e grafici è utile per trovare rapidamente il tipo di grafico che fa per te;
se te la senti, i molti libri di Edward Tufte, che spesso sono delle vere e proprie opere d’arte, o di Alberto Cairo.
documenti e siti web:
ovviamente, il sito di ggplot2 con link a tutto quello che vi può servire
un interessante blog sulla grafica scientifica e non
una bella gallery di grafici con R, forse con un po’ troppa pubblicità (ma è una buona fonte di ispirazione). Non dimenticate di dare uno sguardo alla pagina sui grafici interattivi
la pagina di plotly, una library per grafici interattivi molto potente
una cheatsheet interessante sull’uso dei colori in R http://www.stat.columbia.edu/~tzheng/files/Rcolor.pdf
Video:
un video grazioso sull’uso di grafici nella ricerca biologica
e d’altra parte, se sei un* student* di dottorato avrai sicuramente già letto qualche buon manuale di stile per la scrittura di articoli scientifici↩︎
in Italiano, al solito c’è poco, ma io trovo belli i libri di Emilio Matricciani, cercatelo in libreria o sulle principali piattaforme di vendita online.↩︎
in qualche modo, quando scriviamo o facciamo una presentazione vogliamo “intrattenere” il nostro pubblico e mantenerlo interessato, piuttosto che annoiarlo a morte↩︎
si veda Alberto Cairo, L’arte funzionale, Pearson↩︎
questa è una delle ragioni per cui usare troppi simboli diversi o troppi colori in un grafico scientifico, specialmente se deve essere mostrato per un tempo breve, non ha senso↩︎
Cleveland, W.S., McGill, R., 2012. Graphical Perception: Theory, Experimentation, and Application to the Development of Graphical Methods. J Am Stat Assoc 79, 531–554. https://doi.org/10.1080/01621459.1984.10478080↩︎
in RStudio i grafici compariranno nel riquadro Plots↩︎
viene installato come dependency da molti altri pacchetti importanti↩︎
oppure ad un file, vedi dopo↩︎
vedremo dopo che puoi agire con una certa precisione sulle dimensioni del device e, se lo desideri, dividerlo↩︎
una discussione molto chiara ed estensiva dei diversi formati è qui↩︎
però una descrizione dettagliata delle aree del device grafico è qui↩︎
prova a eseguire
dev.size()e poi ridimensionare ilplot paneed eseguire di nuovo il comando↩︎il segno + deve essere alla fine di ogni comando e non all’inizio della riga del comando successivo! Provare per credere!↩︎
deprecato significa che la funzione non viene più sviluppata negli aggiornamenti del pacchetto; tuttavia, le funzioni deprecate restano spesso disponibili, anche se possono generare dei messaggi di avviso (warning).↩︎
nota come i dati possono essere generati al volo, usando filtri, selezioni o applicando funzioni↩︎
altre possibilità, presenti nella grafica di base ma non in
ggplot2, sono i diagrammi a torta e quelli a mosaico, vedi paragrafo 7.7.2↩︎se proprio sei pigr*, alcune domande interessanti potrebbero essere: che tipo di miglioramento (variabile
Improved) mostrano i due gruppi definiti dalla variabileTreatment? Il sesso e l’età dei pazienti hanno un effetto?↩︎nota come in altri casi quando viene usato
color, ocolour, ofillda soli il colore viene attribuito al riempimento dell’elemento, p.es. il colore di un simbolo in un grafico a dispersione; se però si usano entrambi gli estetici,colourdefinisce il colore del bordo efillil riempimento; nei diagrammi a barre bisogna esplicitamente indicarefillper il riempimento↩︎per maggiori dettagli su cowplot clicca qui↩︎
potresti anche trasformare una delle variabili, come i carati, in log(carat), ma è sconsigliabile↩︎
se vuoi saperne di più leggi la relativa voce di Wikipedia in inglese↩︎
inoltre, è possibile ottenere versioni orizzontali di molti grafici generati con
ggplot2usando ggstance↩︎