4 Dati, oggetti, funzioni (e tutto il resto)
v1.3.4 30/10/2023
4.1 Cosa c’è da imparare in questo capitolo.
Che ti piaccia o no, R è un linguaggio e, se vuoi imparare ad usarlo bene, devi impararne almeno i rudimenti. Molti testi introduttivi recentissimi, inclusi R for data science, Just enough R, ModernDive, o anche cose più eterodosse come YaRrr! tendono a confinare gli elementi di base sulla struttura del linguaggio e la sua sintassi in pochi paragrafi, introducendo poi le funzioni più importanti man mano che se ne presenta la necessità. In effetti, soprattutto se si decide di usare quel particolare dialetto di R creato dal tidyverse, un insieme di pacchetti per la scienza dei dati, molto utilizzati, una volta compresi alcuni concetti di base sulle tabelle (data frame in R) e altre strutture di dati si possono certamente affrontare in maniera efficace aspetti come la visualizzazione grafica, le analisi statistiche di base, etc. senza troppe complicazioni.
Come sempre, nella serena consapevolezza che i miei potenziali lettori sono fondamentalmente pigRi ho deciso di fare qualche piccolo compromesso e di strutturare il capitolo in modo che possa essere fruito per parti, e anche in momenti differenti.
Quindi:
se proprio hai fretta o, semplicemente, se hai voglia di lavorare il meno possibile:
leggi (rapidamente, per carità!) la premessa 4.1.2, con qualche richiamo sulla terminologia relativa a dati, variabili, etc.
leggi attentamente almeno la sezione 4.4 sulle strutture di dati: puoi saltare alcuni paagrafi se vuoi; saranno chiaramente indicati
leggi, almeno superficialmente, la sezione 4.8 su indirizzamento e selezione di sottoinsiemi di dati (sono concetti che verranno richiamati più e più volte nei capitoli successivi)
se hai tempo e voglia, e, soprattutto, se sei veramente interessat* a programmare in R, leggi con attenzione tutto il resto e sentiti liber* di ritornare a questo capitolo mano a mano che prosegui nella lettura.
4.1.1 Premessa 1: esperimenti e osservazioni.
Questo materiale è destinato soprattutto a chi si occupa di scienze sperimentali e in particolare in campi legati alla biologia, biotecnologia, scienze naturali e scienze agrarie. Se sei quindi un* student* di magistrale (improbabile), un* dottorand* di ricerca, un assegnista o un* borsista di ricerca, un* ricercat* i tuoi dati saranno il risultato di esperimenti più o meno complessi. Lo stesso processo che porta alla raccolta dei dati e alla loro analisi è, o dovrebbe essere, ben strutturato e relativamente complesso (figura 4.1).
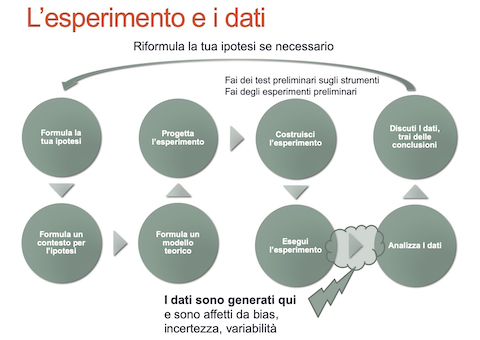
Figura 4.1: Dall’ipotesi sperimentale alle conclusioni.
Il risultato dell’esperimento sono in genere una o più tabelle di dati, più o meno grandi. Se ti occupi di bioinformatica o chemiometria è abbastanza probabile che le tabelle di dati siano veramente grandi o che, addirittura, tu ti trovi a condurre, in una prima fase, delle analisi sperimentali su flussi di dati, magari generati da complessi di sensori, che hanno le caratteristiche dei big data (volume, varietà, velocità, ma anche valore e veracità). Per, esempio, se ti stai occupando di sviluppare un metodo per identificare i determinanti della qualità dei formaggi66 potresti trovarti a disporre di tabelle contenenti dati di composizione bruta (grasso, proteine, etc., in genere da poche a poche decine di variabili), dati sulla composizione in composti volatili (centinaia di variabili), dati spettroscopici (NIR, FTIR, etc., centinaia o migliaia di potenziali variabili), dati sulla composizione del microbiota (potenzialmente centinaia di variabili) su un numero di osservazioni (i formaggi che analizzi) molto inferiore a quello delle variabili. Ammesso che tu abbia progettato ed eseguito correttamente l’esperimento (o, semplicemente, stia utilizzando un approccio più o meno descrittivo e quasi-sperimentale) i tuoi dati saranno invariabilmente affetti da bias (magari legati a strumenti mal calibrati), incertezza (magari dovuta a scarsa sensibilità degli strumenti o degli approcci sperimentali) e variabilità (i dati chimico-biologici sono, per loro natura variabili). Vorrai quindi rappresentare adeguatamente questi dati, riassumendoli, ed estrarne l’informazione rilevante relativamente all’ipotesi scientifica che hai formulato. Se stai usando approcci multivariati complessi, oltre a bias, incertezza e variabilità, le informazioni scientificamente e tecnologicamente irrilevanti potrebbero essere nascosti in mezzo ad una marea di informazioni irrilevanti o non interpretabili: il segnale che ti interessa potrebbe essere il classico ago nel pagliaio (figura 4.2).
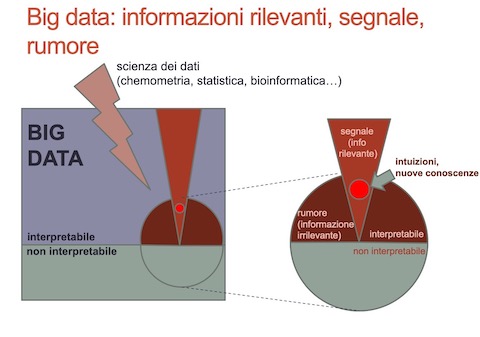
Figura 4.2: Big data e scienze sperimentali: l’ago nel pagliaio. La figura è modificata da Szymańska, E., 2018.
Mentre l’analisi statistica e grafica possono aiutarti a rappresentare correttamente e onestamente i dati e a estrarne un senso, ricorda sempre che sono le ipotesi scientifiche (basate su una robusta conoscenza del campo d’indagine) a guidare la raccolta dei dati e la loro interpretazione e che non c’è analisi che possa migliorare dei dati di cattiva qualità o del tutto irrilevanti per l’ipotesi sperimentale.
4.1.2 Premessa 2. Misure e dati, osservazioni e variabili, tabelle.
Credo di aver già detto che questo non è, e non aspira ad essere, un libro di statistica. Ma se ti trovi nella condizione di non aver mai letto un libro di statistica è bene definire alcuni termini senza i quali è difficile parlare di calcolo statistico con R.
In questo libro cercherò di usare prevalentemente set di dati disponibili con la versione base di R o inclusi nei pacchetti più importanti. Per forza di cose, alcuni di essi non saranno dati legati alla biologia o alle biotecnologie, ma spero che un effetto secondario della lettura di questo libro possa essere quello di rendere un po’ più flessibile il tuo atteggiamento verso i dati in generale.
Per iniziare cominciamo ad esplorare qualche semplice set di dati.
iris è un dataset classico della statistica multivariata. Mostra alcune misure della lunghezza e larghezza di petali e sepali in tre specie del genere Iris.
Il chunk di codice successivo mostra come aprire e visualizzare (nell’interno di questo documento) questo set di dati.
# apre il dataset, che è incluso nell'installazione di base
data("iris")
# mostra il dataset nel tab View del pannello Source in RStudio. Rimuovi il segno
# del commento per eseguire il comando
# View(iris)
# mostra l'aiuto del data set, in alternativa ?iris
# help(iris)
# stampa le prime 20 righe del data set nella Console o, in questo caso, nell'interno del documento
head(iris,20)## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 5.1 3.5 1.4 0.2 setosa
## 2 4.9 3.0 1.4 0.2 setosa
## 3 4.7 3.2 1.3 0.2 setosa
## 4 4.6 3.1 1.5 0.2 setosa
## 5 5.0 3.6 1.4 0.2 setosa
## 6 5.4 3.9 1.7 0.4 setosa
## 7 4.6 3.4 1.4 0.3 setosa
## 8 5.0 3.4 1.5 0.2 setosa
## 9 4.4 2.9 1.4 0.2 setosa
## 10 4.9 3.1 1.5 0.1 setosa
## 11 5.4 3.7 1.5 0.2 setosa
## 12 4.8 3.4 1.6 0.2 setosa
## 13 4.8 3.0 1.4 0.1 setosa
## 14 4.3 3.0 1.1 0.1 setosa
## 15 5.8 4.0 1.2 0.2 setosa
## 16 5.7 4.4 1.5 0.4 setosa
## 17 5.4 3.9 1.3 0.4 setosa
## 18 5.1 3.5 1.4 0.3 setosa
## 19 5.7 3.8 1.7 0.3 setosa
## 20 5.1 3.8 1.5 0.3 setosaUseremo spesso il comando head(), che è un modo rapido per dare uno sguardo ad un data set senza riempire la console; se vuoi inviare alla console le ultime 20 righe puoi usare
>tail(iris, 20)nota che l’alternativa è print(iris); il comando print ha varie opzioni utili, fra cui alcune che regolano giustificazione e numero di cifre significative. Prova, per esempio:
> print(iris, digits = 2)Se vuoi visualizzare il set di dati in RStudio, vedere l’aiuto e “stampare” il data set nella console scrivi i seguenti comandi nella Console (ricordati che non devi scrivere >, perché il prompt appare automaticamente nella Console ogni volta che premi invio e completi un comando).
>data(iris)
>View(iris)
>?iris
>iris4.1.3 Anatomia di una tabella.
Anche se magari queste cose sono scontate, è bene scendere un pochino più in dettaglio nella struttura di questa tabella.

Figura 4.3: Anatomia di una tabella: alcune caratteristiche morfologiche dei fiori di tre specie di iris.
Iris è un dataset storico, utilizzato, fra le altre cose per dimostrare alcune tecniche di analisi multivariata, come l’analisi discriminante lineare. E’ una semplice tabella che contiene 5 variabili67:
quattro variabili quantitative continue68, per scala di rapporti69: lunghezza e larghezza dei petali, lunghezza e larghezza dei sepali;
una variabile qualitativa nominale: il nome delle tre specie del genere Iris messe a confronto. Questa variabile può assumere un numero finito di valori o categorie che non hanno nessun ordine ovvio. In R questo tipo di variabile è chiamata “fattore”.
Le variabili, quindi, corrispondono alle colonne della tabella e le singole osservazioni (eseguite in questo caso ciascuna su una singola unità campionaria) alle righe70. Una singola misura è identificata, in questo caso, dal numero di riga e di colonna o dal numero di riga e dal nome della variabile. Analogamente, ci possiamo riferire a sottoinsiemi di dati usando vettori di numeri di righe e colonne (vedi sezione 4.8.
I dataset di R e delle sue librerie forniscono una messe enorme di esempi. Un dataset che utiizzeremo molto è Arthritis71. Arthritis appartiene alla libreria vcd: per renderlo disponibile è necessario installare e caricare prima questa libreria.
# carica la libreria (in realtà questo avviene in maniera automatica nel setup
# dello script usato per generare questo capitolo)
library(vcd)
# carica il dataset
data("Arthritis")
# stampa il data set nella Console o, in questo caso, nell'interno del documento
head(Arthritis,20)## ID Treatment Sex Age Improved
## 1 57 Treated Male 27 Some
## 2 46 Treated Male 29 None
## 3 77 Treated Male 30 None
## 4 17 Treated Male 32 Marked
## 5 36 Treated Male 46 Marked
## 6 23 Treated Male 58 Marked
## 7 75 Treated Male 59 None
## 8 39 Treated Male 59 Marked
## 9 33 Treated Male 63 None
## 10 55 Treated Male 63 None
## 11 30 Treated Male 64 None
## 12 5 Treated Male 64 Some
## 13 63 Treated Male 69 None
## 14 83 Treated Male 70 Marked
## 15 66 Treated Female 23 None
## 16 40 Treated Female 32 None
## 17 6 Treated Female 37 Some
## 18 7 Treated Female 41 None
## 19 72 Treated Female 41 Marked
## 20 37 Treated Female 48 None# più avanti vedremo delle funzioni che permettono di personalizzare l'aspetto
# di una tabella in un documento, in un report o una presentazioneRicorda che se avessi voluto mostrare il data set nel pannello Source avresti potuto usare View(Arthritis) e se avessi voluto sapere di più su questo data set apresti potuto usare il comando ?Arthritis.
In questo caso si tratta di un dataset che riporta i dati di un test clinico. La prima variabile, ID, nonostante sia in apparenza numerica (in questo caso si tratta di interi) non è altro che un numero che individua univocamente un singolo paziente; è quindi anch’essa una variabile qualitativa nominale (un fattore non ordinato), ma in questo caso i valori sono unici, e non ha senso usare un fattore (che ha un numero limitato di livelli che possono comparire più di una volta). La variabile Treatment è uno dei fattori del disegno sperimentale: è una variabile nominale che ha solo due valori. Lo stesso vale per la variabile Sex. La variabile Age è una variabile quantitativa; tecnicamente può assumere valori continui, ma qui è solo riportata l’età in anni e non, per esempio, in nanosecondi. Quando più avanti parleremo di disegni sperimentali, vedrai che questo è un esperimento sbilanciato (non c’è un uguale numero di pazienti per trattamento) e possiamo immaginare che pazienti, di diverso sesso e età siano stati assegnati in maniera casuale72 a due gruppi (Treated, che hanno ricevuto un trattamento per l’artrite che si immagina debba migliorare il quadro clinico del paziente e Placebo, che hanno ricevuto una sostanza innocua). L’ultima variabile, Improved, è una variabile qualitativa ordinale (un fattore ordinato) con tre livelli73.
4.1.4 Un piccolo esercizio.
Usando lo stesso tipo di comandi prova ad aprire (e a stampare a console) i seguenti dataset e a leggerne l’aiuto:
mtcarso, se preferisci,ggplot2::mpg74DNaseOrangeInsectSpraysCO2
Che tipi di variabili contengono? Ti sembra che siano dati ricavati da semplici osservazioni o risultati di un esperimento realizzato secondo un preciso disegno sperimentale? Più avanti vedremo anche strutture di dati più complesse, divise in varie tabelle o in oggetti a più di due dimensioni75
4.1.5 Tidy vs. untidy (tabelle ordinate e disordinate).
Chiunque, come docente, abbia visto una tabella prodotta da uno studente durante lo svolgimento di una tesi di laurea sperimentale sa cosa voglia dire “dati disordinati” (“untidy”). I dati disordinati sono difficili da visualizzare e analizzare e molti dei comandi che userò in questo libro si “aspettano” dati ordinati (“tidy”). Il concetto di “tidy data” è stato descritto in maniera eccellente da Hadley Wickham, una sorta di semidio del mondo di R. Per metterla in modo semplice, in un set di dati tidy:
ogni colonna è una variabile
ogni riga è un’osservazione
ogni cella è una misura
Molto spesso, in un set di dati “tidy” è facile individuare sottotabelle di dati “tidy”, identificate da combinazioni di valori di variabili qualitative. Pensate per esempio ai due dataset iris e Arthritis. Osservate le seguenti tabelle, riordinate per mettere in evidenza la struttura “tidy”.
# non badate ai comandi, tutti del pacchetto dplyr appartenente al tidyverse,
# imparerete come usarli nei capitoli successivi
# se non lo avete già fatto prima caricate il pacchetto dplyr con
# require(dplyr)
# qui head() è usato per stampare alcune righe
Arthr <- Arthritis %>% arrange(Treatment, Sex, Improved)
head(Arthr,20)## ID Treatment Sex Age Improved
## 53 80 Placebo Female 23 None
## 54 12 Placebo Female 30 None
## 55 29 Placebo Female 30 None
## 57 38 Placebo Female 32 None
## 59 51 Placebo Female 37 None
## 60 54 Placebo Female 44 None
## 61 76 Placebo Female 45 None
## 62 16 Placebo Female 46 None
## 63 69 Placebo Female 48 None
## 64 31 Placebo Female 49 None
## 65 20 Placebo Female 51 None
## 66 68 Placebo Female 53 None
## 67 81 Placebo Female 54 None
## 68 4 Placebo Female 54 None
## 71 49 Placebo Female 57 None
## 76 48 Placebo Female 61 None
## 78 3 Placebo Female 64 None
## 80 32 Placebo Female 66 None
## 81 42 Placebo Female 66 None
## 56 50 Placebo Female 31 Some## Species Sepal.Length Sepal.Width Petal.Length Petal.Width
## 1 setosa 5.1 3.5 1.4 0.2
## 2 setosa 4.9 3.0 1.4 0.2
## 3 setosa 4.7 3.2 1.3 0.2
## 4 setosa 4.6 3.1 1.5 0.2
## 5 setosa 5.0 3.6 1.4 0.2
## 6 setosa 5.4 3.9 1.7 0.4
## 7 setosa 4.6 3.4 1.4 0.3
## 8 setosa 5.0 3.4 1.5 0.2
## 9 setosa 4.4 2.9 1.4 0.2
## 10 setosa 4.9 3.1 1.5 0.1
## 11 setosa 5.4 3.7 1.5 0.2
## 12 setosa 4.8 3.4 1.6 0.2
## 13 setosa 4.8 3.0 1.4 0.1
## 14 setosa 4.3 3.0 1.1 0.1
## 15 setosa 5.8 4.0 1.2 0.2
## 16 setosa 5.7 4.4 1.5 0.4
## 17 setosa 5.4 3.9 1.3 0.4
## 18 setosa 5.1 3.5 1.4 0.3
## 19 setosa 5.7 3.8 1.7 0.3
## 20 setosa 5.1 3.8 1.5 0.3Notate come, scorrendo le tabelle, è possibile individuare facilmente le sottotabelle: in iris ogni valore della variabile Species definisce una sottotabella. In Arthritis ogni combinazione di una o più delle variabili Treated, Sex e Improved definisce una o più sottotabelle.
Sfortunatamente, non tutti i dati sono “tidy”. Osservate il dataset billboard del pacchetto tidyr.
## # A tibble: 25 × 79
## artist track date.entered wk1 wk2 wk3 wk4 wk5 wk6 wk7 wk8
## <chr> <chr> <date> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 2 Pac Baby… 2000-02-26 87 82 72 77 87 94 99 NA
## 2 2Ge+her The … 2000-09-02 91 87 92 NA NA NA NA NA
## 3 3 Doors D… Kryp… 2000-04-08 81 70 68 67 66 57 54 53
## 4 3 Doors D… Loser 2000-10-21 76 76 72 69 67 65 55 59
## 5 504 Boyz Wobb… 2000-04-15 57 34 25 17 17 31 36 49
## 6 98^0 Give… 2000-08-19 51 39 34 26 26 19 2 2
## 7 A*Teens Danc… 2000-07-08 97 97 96 95 100 NA NA NA
## 8 Aaliyah I Do… 2000-01-29 84 62 51 41 38 35 35 38
## 9 Aaliyah Try … 2000-03-18 59 53 38 28 21 18 16 14
## 10 Adams, Yo… Open… 2000-08-26 76 76 74 69 68 67 61 58
## # ℹ 15 more rows
## # ℹ 68 more variables: wk9 <dbl>, wk10 <dbl>, wk11 <dbl>, wk12 <dbl>,
## # wk13 <dbl>, wk14 <dbl>, wk15 <dbl>, wk16 <dbl>, wk17 <dbl>, wk18 <dbl>,
## # wk19 <dbl>, wk20 <dbl>, wk21 <dbl>, wk22 <dbl>, wk23 <dbl>, wk24 <dbl>,
## # wk25 <dbl>, wk26 <dbl>, wk27 <dbl>, wk28 <dbl>, wk29 <dbl>, wk30 <dbl>,
## # wk31 <dbl>, wk32 <dbl>, wk33 <dbl>, wk34 <dbl>, wk35 <dbl>, wk36 <dbl>,
## # wk37 <dbl>, wk38 <dbl>, wk39 <dbl>, wk40 <dbl>, wk41 <dbl>, wk42 <dbl>, …Il database contiene i dati della posizione in classifica di diverse canzoni in diverse settimane a partire dal rilascio. E’ abbastanza ovvio che la variabile “tempo” non esiste e questo rende difficile, per esempio, rappresentare graficamente l’andamento della posizione della canzone nel tempo. tidyr contiene molti altri esempi illustrativi di altre situazioni di dati untidy. Talvolta, trasformare i dati da “untidy” a “tidy” è una vera e propria lotta (“data wrangling”) o meglio, una vera e propria arte78, e ce ne occuperemo nel capitolo 9.
4.1.6 Dati mancanti (missing data).
In billboard, e in molti altri set di dati, ci sono dati mancanti (missing values). Nel dialetto di R i dati mancanti79 si indicano come NA, not available, e la loro presenza può impedire il calcolo di statistiche o l’analisi di modelli, se non sono opportunamente trattati o eliminati.
Nelle scienze sperimentali i dati possono essere mancanti per diverse ragioni:
in un esperimento, i dati per alcune ripetizioni di un trattamento possono andare perduti perché va perduto un campione, per il malfunzionamento di uno strumento, l’imperizia di un operatore: questo può rendere sbilanciati80 esperimenti che erano bilanciati o, nei casi peggiori, portare alla perdita di tutti i dati di un trattamento;
in un’analisi descrittiva o in un set di dati quasi sperimentale possono mancare (perché non disponibili nel campione che è stato raccolto) i dati corrispondenti a determinate combinazioni di variabili esplicative, o, anche in questo caso, i dati possono andare perduti per il malfunzionamento di sensori e strumenti;
in un sondaggio o in un esperimento di analisi sensoriale i partecipanti potrebbero non fornire alcune delle risposte attese;
Inoltre, i dati possono essere mancanti in modo esplicito (sappiamo che ci sono dei dati mancanti e lo indichiamo esplicitamente nella nostra tabella, usando, appunto NA) o implicito (sappiamo che dei valori dovrebbero essere presenti, per esempio dai valori di altre osservazioni o variabili ma non ci sono, pur non essendo esplicitamente assenti)81.
## anno vendite
## 1 1999 100
## 2 2000 NA
## 3 2001 101
## 4 2002 102## anno vendite
## 1 1999 100
## 2 2001 101
## 3 2002 102Come vedi, nel secondo data frama manca l’anno 2000: questo è chiaro nel primo data frame, perché il valore NA compare nella colonna vendite, ma non qui.
Proprio per l’importanza dei dati mancanti nelle analisi statistiche esistono varie tecniche per individuarli82, di studiarne la distribuzione (sono mancanti “a caso” o esiste un pattern?), di “tradurne” l’esistenza (diversi tipi di tabelle possono indicare i dati mancanti in modo diverso, per esempio come celle vuote, spazi, punti, etc.) durante l’importazione di file o addirittura di tentare un’imputazione. Come sempre, in R esistono funzioni e addirittura pacchetti dedicati83 a questo scopo. Ti consiglio almeno di leggere la voce dell’aiuto di R sui dati mancanti. Nota che NA non è la stessa cosa di NaN84 e NULL. Prova con questo codice nella console:
?NA
sqrt(-2)
?NULLSi tratta di tre valori molto fastidiosi (generano warning o addirittura errori, che possono arrestare l’esecuzione di uno script) ma anche sorprendentemente utili nella programmazione.
4.2 R è un linguaggio funzionale che supporta la programmazione orientata a oggetti…
Appunto, qualsiasi cosa questo voglia dire…85. Come me, probabilmente non sei un programmatore esperto, ma, per usare R, occorre imparare un po’ di terminologia sulle funzioni e sugli oggetti. In R, tutto quello che esiste (e cui può essere attribuito un valore) è un oggetto (e gli oggetti hanno classi e attributi che li descrivono), mentre tutto quello che accade, accade perché hai invocato una una funzione86.
Fondamentalmente, per poter lavorare è importante capire (bene) alcune cose:
per poter “trovare” un oggetto nell’ambiente di lavoro è necessario usare un nome (è l’oggetto che viene attribuito ad un nome e non viceversa, vedi l’esempio successivo)
gli oggetti vengono assegnati ai nomi con l’operazione di assegnazione (usando le funzioni
<-->=
esistono diverse classi di oggetti, incluse le strutture di dati (che sono quelle su cui operiamo nelle analisi); la classe è uno degli attributi degli oggetti, e gli attributi sono una sorta di metadati che aiutano a definirne proprietà e comportamenti di un oggetto
la classe di un oggetto (che si può “interrogare” con la funzione
class()) definisce il comportamento dell’oggetto quando quest’ultimo viene usato da diverse funzioni generiche (come per esempioprint()oplot(), che si comportano in modo diverso quando hanno come argomento oggetti di classi diverse)oltre alla classe gli oggetti hanno altri attributi, come nomi, dimensioni, etc. che possono essere “interrogati” o definiti usando le funzioni appropriate
## [1] 1# 1L è un vettore intero di lunghezza 1
c(1, 2, 3) # un altro oggetto, un vettore numerico a precisione doppia di lunghezza 3## [1] 1 2 3# l'assegnazione dell'oggetto al nome a, l'istruzione assegna ma non stampa a console
a <- 1L
# stampa a console il valore di a
a ## [1] 1## [1] 1## [1] "integer"## [1] "integer"# tre modi validi, per assegnare, ma il primo è preferibile perché meno ambiguo
# il metodo migliore
b <- c(1, 2, 3)
# funziona anche questo ma si confonde con l'assegnazione di valori a parametri di funzioni
b = c(1, 2, 3)
# funziona ma è difficile da leggere
c(1, 2, 3) -> b
b## [1] 1 2 3## [1] 1## [1] 1 2 3## [1] "numeric"## [1] "double"# altri attributi importanti sono la dimensione
# che (ha senso per gli oggetti a 2 o più dimensioni)
dim(Arthritis)## [1] 84 5## [1] 3# alcuni oggetti hanno nomi per i singoli elementi o per le diverse dimensioni
vettore_con_nomi <- c(a = 1, b = 2, c = 3)
names(vettore_con_nomi)## [1] "a" "b" "c"## [1] "ID" "Treatment" "Sex" "Age" "Improved"## [1] "1" "2" "3" "4" "5" "6" "7" "8" "9" "10" "11" "12" "13" "14" "15"
## [16] "16" "17" "18" "19" "20" "21" "22" "23" "24" "25" "26" "27" "28" "29" "30"
## [31] "31" "32" "33" "34" "35" "36" "37" "38" "39" "40" "41" "42" "43" "44" "45"
## [46] "46" "47" "48" "49" "50" "51" "52" "53" "54" "55" "56" "57" "58" "59" "60"
## [61] "61" "62" "63" "64" "65" "66" "67" "68" "69" "70" "71" "72" "73" "74" "75"
## [76] "76" "77" "78" "79" "80" "81" "82" "83" "84"## [1] "a" "b" "c"## a b c
## 1 2 3## d e f
## 1 2 34.3 Il nome delle cose.
In R ci sono poche limitazioni sui nomi degli oggetti87:
possono contenere lettere, numeri, “_” e “-” in qualsiasi combinazione
non possono contenere spazi
non devono iniziare con un numero, “_” o “-”
non devono corrispondere a un nome “riservato”, cioé a uno dei nomi utilizzati dal linguaggio
R è un linguaggio case-sensitive (maiuscole e minuscole non sono la stessa cosa, quindi a e A o anova() e Anova() non sono la stessa cosa). In sostanza, puoi fare un po’ quello che ti pare anche se, ovviamente esistono delle guide di stile alle quali sarebbe bene uniformarsi, se non altro per coerenza e per aumentare la leggibilità del codice che scrivi (per gli altri e per il tuo io futuro). Due esempi sono la guida di Google e quella del tidyverse. Io, per ragioni religiose, cercherò di seguire quella del tidyverse (un universo ordinato di pacchetti molto utili), ma, siccome sono smemorato e incoerente potrei dimenticarmene di quando in quando.
Quelli che seguono sono alcuni esempi di convenzioni sull’assegnazione di oggetti a nomi:
# un nome valido: è bene che i nomi siano descrittivi e che dal nome si possa capire
# per quanto possibile, che cos'é l'oggetto: questo aiuta molto nella lettura del codice
il_mio_nome <- "Maurizio"
# ma va bene anche
il_mio_nome <- c(1,2,3)
# in fondo, R che ne sa?
# lo stesso oggetto con 2 nomi
c <- d <- 3L
# maiuscole e minuscole non sono la stessa cosa
C <- 4L
# cat() è una funzione molto utile per documentare ciò che va in console
# \n permette di inserire un daccapo;
cat("\nil valore di c piccolo è\n")##
## il valore di c piccolo è## [1] 3##
## il valore di C grande è## [1] 4# è bene dare nomi descrittivi agli oggetti
il_mio_nome <- "Maurizio"
# questo va bene e l'uso di _ per separare parole di chiama "snake case"
# questi funzionano ma vanno meno bene
ilmionome <- "Silvio"
ILMIONOME <- "Giorgia"
IlMioNome <- "Matteo"
# questo si chiama "camel case" perché le maiuscole assomigliano
# alle gobbe di un cammello
# per le funzioni è meglio usare verbi
fai_la_somma <- function(a=1, b=2, c=3) a+b+c
cat("\nla somma di 5, 6 e 7 è\n")##
## la somma di 5, 6 e 7 è## [1] 18Come vedrai più avanti \ è il segno di escape e si può usare per individuare caratteri speciali; \t, per esempio, è una tabulazione.
Per sperimentare con i nomi non sintattici prova a scrivere ed eseguire questo script:
# un nome sbagliato, non sintattico
1schifodinome <- 1
# restituisce un errore
`1schifodinome` <- 1
`1schifodinome`
# questo funziona, ma è uno schifo
# questo piccolo trucco può venire comodo nell'importazione di dati da altri
# software che non hanno questo tipo di limitazioniPensa a quante tabelle, fatte male, hanno intestazioni di colonna (e quindi nomi di variabili) non sintattici, e ai dolori di pancia per importarle…
In questo libro, per coerenza, farò il possibile per usare nomi in italiano. E’ abbastanza ovvio che se vuoi che il tuo codice sia letto e compreso da altri, devi assegnare nomi che abbiano senso in inglese.
Descrivere il modo in cui R cerca i valori associati ad un determinato nome (sia esso il nome di una funzione o il nome di una struttura di dati) è troppo complesso per un libro introduttivo come questo. Probabilmente, quando imparerai a programmare meglio dovrai approfondire questo argomento. Come al solito, un ottimo punto di partenza è Advanced R. Qui ti basti ricordare che, per quanto in generale non sia necessario essere molto specifici, quando esiste un’ambiguità (è possibile per esempio che diversi pacchetti abbiano funzioni con lo stesso nome, o è possibile che una variabile con lo stesso nome sia presente in tabelle diverse) bisogna stare attenti ad indicare con precisione dove cercare. Vedremo alcuni esempi in seguito.
4.4 Strutture di dati.
Le strutture di dati sono quelle che importerai, aprirai, userai per le analisi, salverai, etc. e, che, per l’appunto contengono dati. Possiamo distinguerle in
vettori atomici (atomic vectors): contengono dati di un solo tipo (vedi dopo)
a una dimensione: vettori (vectors)
a due dimensioni: matrici (matrices)
a n dimensioni: array
vettori generici (generic vectors): possono contenere più tipi di dati
data frames: possono contenere vettori di diverso tipo, con il vincolo che tutti siano della stessa lunghezza. I data frames sono, in realtà, liste con alcuni vincoli (tutti gli elementi devono avere la stessa lunghezza). Vedremo più avanti che è anche possibile avere data frame annidati, con colonne che contengono altri data frame. Come hai già visto i data frame sono il tipo di tabella che userai più frequentemente, per la loro versatilità. Esiste una versione “aggiornata” dei data frame, fornita dal pacchetto
tibble, che a sua volta fa parte deltidyverse, chiamata appuntotibble.liste (lists): sono gli oggetti più flessibili di tutti, perché possono contenere oggetti di qualsiasi tipo e lunghezza, incluse altre liste; come vedrai, oltre a contenere dati, possono contenere risultati di analisi e persino grafici.
4.5 Vettori atomici.
La struttura di base per i dati in R è il vettore, un insieme ordinato di dati, che, nei vettori atomici, sono necessariamente dello stesso tipo. In R non esistono scalari: gli scalari sono vettori di lunghezza 1.
4.5.1 Vettori ad una dimensione.
Gli elementi di un vettore ad una dimensione sono messi insieme dalla funzione c(), che, appunto, concatena elementi.
Ogni vettore atomico contiene elementi dello stesso tipo (type) o modo (mode). I tipi più frequentemente utilizzati sono:
numerici: interi, p.es.
c(1L, 2L, 3L); doppi, p. es.c(1.25, -3.14, 999)88logici: con elementi che possono assumere solo i valori
TRUE(oT) oFALSE(oF)89carattere: contengono per l’appunto, simboli che sono interpretati come caratteri, e che devono essere inseriti fra virgolette, singole o doppie:
c("a", "Apple", "1", "TRUE"); nota come il terzo elemento di questo vettore è un numero, ma è interpretato come carattere; il quarto è un valore logico ma, essendo fra virgolette, viene interpretato come carattere.
Una classe particolare di vettori sono i fattori (factors). I fattori sono particolarmente utili per le variabili nominali o ordinali con un numero limitato di valori diversi (vedi il paragrafo 4.1.3). I fattori sono in realtà conservati in memoria come vettori di interi, cui sono associati dei nomi dei livelli e, eventualmente, il loro ordine.
Esistono comandi specifici per creare i diversi tipi di vettori, e li vedrai negli esempi successivi.90
E’ possibile “interrogare” un oggetto usando diverse funzioni, come nell’esempio successivo. E’ anche possibile usare alcune funzioni per “costringere” un oggetto a cambiare tipo (si chiama coercizione e, qualche volta, R la fa in automatico).
Interrogare oggetti e cambiarne il tipo possono sembrare operazioni futili se ci si immagina di lavorare con R solo in modo interattivo: in fondo, se siamo lì a guardare dovremmo sapere benissimo quello che sta succendendo, no? Tuttavia, la potenza di R si scatena veramente solo quando lo usiamo per creare programmi e script e per automatizzare operazioni: in questo caso, potrebbe essere necessario che R chieda per conto nostro ad un’oggetto di che tipo è e lo converta se necessario in un altro tipo. Infatti, alcune funzioni accettano solo oggetti di un certo tipo e non è sempre ovvio o noto con che tipo di oggetto abbiamo a che fare91.
## [1] 1 2 3## [1] "numeric"## [1] "double"## [1] 3## NULL## d e f
## 1 2 3## [1] "numeric"## [1] "d" "e" "f"# nota che il risultato di names() può essere assegnato
i_nomi <- names(vettore_con_nomi)
# che vettore abbiamo creato? di che classe, lunghezza, tipo?
# un modo semplice per conoscere gli attributi
attributes(vettore_con_nomi)## $names
## [1] "d" "e" "f"# che tipo di oggetto restituisce attributes()? Prova ad usare l'aiuto...
# con la funzione c() possiamo anche concatenare vettori. Vediamo che succede:
vettori_concatenati <- c(a,b)
class(vettori_concatenati)## [1] "numeric"## [1] "double"# nota come questo sia un vettore carattere; eccone altri
il_mio_TESTO <- c("A","B","C")
il_mio_testo <- c("a","b","c")
# nota che questo non è lo stesso oggetto e che anche i nomi sono diversi
# naturalmente è possibile creare un vettore logico direttamente
logico <- c(TRUE, FALSE, FALSE)
# ma anche
logico <- c(T, F, F)
# alcune funzioni usate per interrogare oggetti restituiscono valori logici
is.numeric(a)## [1] TRUE## [1] TRUE## [1] FALSE# i fattori sono molto importanti, sia per ragioni storiche, sia perché sono il
# prototipo delle variabili categoriche
# creiamo un fattore non ordinato (il default)
fattore_non_o <- factor(c("vowel","consonant","consonant"))
# la funzione str() ci dice qualcosa sulla struttura di quest'oggetto
str(fattore_non_o)## Factor w/ 2 levels "consonant","vowel": 2 1 1# come vedi, di default R ha assegnato il livello in ordine alfabetico
# nota anche come, in realtà, i valori siano conservati come interi (1, 2)
# mentre i nomi dei livelli sono attributi
# prova a leggere l'aiuto di factor() e as-factor()
# guarda cosa succede con una variabile ordinale, se non stiamo attenti
quanto <- factor(c("molto", "molto", "poco", "moltissimo", "abbastanza"))
quanto## [1] molto molto poco moltissimo abbastanza
## Levels: abbastanza moltissimo molto poco## Factor w/ 4 levels "abbastanza","moltissimo",..: 3 3 4 2 1# sarebbe ovviamente desiderabile che ci fosse un ordine logico:
# in fondo poco è meno abbastanza, che è meno di molto che è meno di moltissimo
# a questo punto i default della funzione factor() non bastano, e dobbiamo essere
# più specifici, indicando i livelli:
quanto_ord <-factor(c("molto", "molto", "poco", "moltissimo", "abbastanza"),
levels = c("poco", "abbastanza", "molto", "moltissimo"),
ordered = T)
quanto_ord## [1] molto molto poco moltissimo abbastanza
## Levels: poco < abbastanza < molto < moltissimo## Ord.factor w/ 4 levels "poco"<"abbastanza"<..: 3 3 1 4 2## [1] "integer"## $levels
## [1] "poco" "abbastanza" "molto" "moltissimo"
##
## $class
## [1] "ordered" "factor"Vedremo più avanti come lavorare con i fattori non sia sempre semplicissimo e che, ancora una volta per ragioni storiche, possa capitare che un vettore di caratteri venga convertito in un fattore in maniera esplicita o “dietro le quinte”.
Nota che è buona pratica di programmazione dividere in maniera logica su più linee un singolo comando molto lungo; se non sei cert* come farlo, prova a selezionare il comando o la parte di codice che vuoi formattare correttamente e poi usa il menu
L’esempio successivo illustra alcuni aspetti dell’uso di caratteri speciali nei vettori a carattere e fornisce qualche dettaglio in più sulla coercizione. Potrebbe essere utile in diverse situazioni ma, se vuoi, puoi saltarlo.
# caratteri speciali
# in alcuni casi potrebbe essere necessario aggiungere caratteri speciali al testo
# aggiungere esplicitamente delle virgolette
virgolettato <- c("'A'", "'B'", "'C'")
virgolettato## [1] "'A'" "'B'" "'C'"## [1] "\"A\"" "\"B\"" "\"C\""# degli a capo (per inserire tabulazioni puoi usare \t)
a_capo <- "A\nB\nC"
# altri modi di stampare
# nota come diversi comandi possano stampare contenuto o contenuto "grezzo"
print(virgolettato)## [1] "'A'" "'B'" "'C'"## 'A' 'B' 'C'## A
## B
## Ccat() e writelines() possono anche inviare il risultato a altre “connessioni”, cioé ad un file piuttosto che alla console; è in qualche maniera un residuo dei bei vecchi tempi, non credo che valga la pena parlarne, ma, se vuoi leggi qui o qui.
Vediamo ora qualche esempio di coercizione. Che succede se provo a concatenare oggetti di tipo diverso (uno numerocio e uno a caratteri)?
## [1] "1" "2" "3" "1" "2" "3" "d" "e" "f"## [1] "character"## [1] "character"Il risultato è un vettore di tipo carattere: R ha esercitato quella che si chiama coercizione; è possibile convertire praticamente tutto in caratteri, ma non viceversa.
## [1] "1" "2" "3" "1" "2" "3"## [1] "character"Nota come posso annidare due funzioni una dentro l’altra; il risultato del comando
typeof(as.character(vettori_concatenati))
É trasformare un vettore numerico in un vettore carattere (senza assegnarlo a un nome) e, contemporaneamente, leggerne il tipo. Nota che questa non è buona pratica di programmazione perché il codice potrebbe essere poco leggibile. Prova a scrivere a console il seguente comando
as.numeric(i_nomi)La coercizione può avvenire anche come risultato di operazioni, guarda che succede qui sotto:
# controlliamo se il contenuto dei due oggetti è identico, elemento per elemento, con la funzione ==
il_mio_TESTO == il_mio_testo## [1] FALSE FALSE FALSE# cosa restituisce quest'operazione? Che lunghezza ha il risultato?
# Controlliamo, assegnando il risultato ad un vettore
risultato <- (il_mio_TESTO == il_mio_testo)
class(risultato)## [1] "logical"## [1] "logical"## [1] 3# il risultato è un vettore logico di lunghezza 3, perché sono stati fatti 3 confronti
# oppure possiamo usare le funzioni as.xxxx()
as.factor(il_mio_testo)## [1] a b c
## Levels: a b c## [1] 1 0 0## [1] "1" "2" "3"## [1] "molto" "molto" "poco" "moltissimo" "abbastanza"## [1] TRUE FALSE TRUE FALSE4.5.2 Vettori atomici a 2 o più dimensioni: matrici e array.
Nella pratica incontrerai prevalentemente strutture di dati a 2 (righe = osservazioni, colonne = variabili) o più (per esempio, righe = osservazioni, colonne = variabili, strati = tempo o luogo nel quale sono state eseguite le misure, identità del soggetto su cui sono state eseguite le misure). Vedrai in seguito come gli oggetti a più di due dimensioni possano essere facilmente trasformati, usando una o più variabili indice per individuare le sottotabelle, in oggetti a 2 dimensioni corrispondenti agli strati degli oggetti a più dimensioni. In R i vettori atomici a due dimensioni sono chiamati matrici e vengono creati:
con il comando
matrix()estraendo colonne dello stesso tipo da un data frame e usando
as.matrix()92come risultato di analisi statistiche: per esempio la funzione
cor()accetta una matrice numerica e restituisce una matrice di correlazione sempre numerica
Il comando matrix() prende come input un insieme di dati della dimensione opportuna e lo trasforma in una matrice con un numero di righe e colonne specificato, riempiendo la matrice per colonne (il default) o per righe, e assegna opzionalmente i nomi di righe e colonne. Il comando array() fa lo stesso per gli array.
Prova a esplorare l’aiuto scrivendo nella console:
>?matrix
>?arrayOppure studia con attenzione questo esempio (anche se sei pigr*).
Introduco rapidamente il comando seq(), che crea una sequenza numerica. Il comando ha molte opzioni ed è molto flessibile. Nella versione più semplice # crea una sequenza di uno in 1.
## [1] 1 2 3 4 5 6 7 8 9## [1] 1 2 3 4 5 6 7 8 9## [1] 1 2 3 4 5 6 7 8 9# una matrice 3x3 riempita per colonne
per_colonne <- matrix(seq(1,9), nrow =3, ncol= 3,
dimnames = list(c("A","B","C"),c("D","E","F")))
per_colonne## D E F
## A 1 4 7
## B 2 5 8
## C 3 6 9# che succede se il vettore ha la dimensione sbagliata?
per_colonne_sbagliato <- matrix(seq(1,10), nrow =3, ncol= 3,
dimnames = list(c("A","B","C"),c("D","E","F")))## Warning in matrix(seq(1, 10), nrow = 3, ncol = 3, dimnames = list(c("A", : data
## length [10] is not a sub-multiple or multiple of the number of rows [3]per_colonne_sbagliato_2 <- matrix(seq(1,8), nrow =3, ncol= 3,
dimnames = list(c("A","B","C"),c("D","E","F")))## Warning in matrix(seq(1, 8), nrow = 3, ncol = 3, dimnames = list(c("A", : data
## length [8] is not a sub-multiple or multiple of the number of rows [3]Nota come nel primo caso un valore è rimasto fuori e nel secondo il primo valore della sequenza è stato riciclato: questo è un comportamento frequente di R, che cerca di effettuare, per quanto possibile, le operazioni richieste, anche se gli argomenti sono errati o incompleti: quando comunque è possibile restituire un valore, viene restituito anche un warning che non arresta l’eventuale esecuzione di un programma, altrimenti viene restituito un errore.
Ora proviamo a riempire la stessa matrice per righe:
per_righe <- matrix(seq(1:9),
nrow =3, ncol= 3, byrow = T,
dimnames = list(c("A","B","C"),c("D","E","F")))
per_righe## D E F
## A 1 2 3
## B 4 5 6
## C 7 8 9# ovviamente è possibile creare matrici di valori carattere o logici o interi
matrice_logica <- matrix(c(logico, logico, logico),
nrow =3, ncol= 3, byrow = T,
dimnames = list(c("A","B","C"),c("D","E","F")))
matrice_logica## D E F
## A TRUE FALSE FALSE
## B TRUE FALSE FALSE
## C TRUE FALSE FALSEL’argomento data della funzione matrix() può essere anche un vettore definito in precedenza o estratto dall’ambiente di lavoro. Nota l’uso della funzione rep(), che crea ripetizioni con pattern anche complessi.
si9 <- rep("Yes",9)
dimmi_di_si <- matrix(si9, nrow= 3, ncol = 3)
mantra <- rep(c("amore","pace"),6)
matrice_carattere <- matrix(mantra,
nrow =3, ncol= 2, byrow = T,
dimnames = list(c("A","B","C"),c("A","B")))## Warning in matrix(mantra, nrow = 3, ncol = 2, byrow = T, dimnames = list(c("A",
## : data length differs from size of matrix: [12 != 3 x 2]Nota in che modo vengono stampate le matrici:
## D E F
## A 1 4 7
## B 2 5 8
## C 3 6 9## A B
## A "amore" "pace"
## B "amore" "pace"
## C "amore" "pace"## D E F
## A TRUE FALSE FALSE
## B TRUE FALSE FALSE
## C TRUE FALSE FALSELe matrici hanno come attributi importanti i nomi di riga e colonna (devono essere unici ma una colonna può avere lo stesso nome di una riga) e le dimensioni.
## [1] "matrix" "array"## [1] "character"## chr [1:3, 1:2] "amore" "amore" "amore" "pace" "pace" "pace"
## - attr(*, "dimnames")=List of 2
## ..$ : chr [1:3] "A" "B" "C"
## ..$ : chr [1:2] "A" "B"## [1] 3 2Cosa restituisce la funzione dim()? Anche se non lo sai, puoi determinarlo con una delle funzioni che abbiamo già usato?
Il funzionamento della funzione array() è simile:
# creo un array 3x4x3
array_per_colonne <- array(seq(1:36),
dim = c(3,4,3),
dimnames = list(c("A","B","C"),c("D","E","F","G"),
c("X","Y","Z")))
# nota come viene riempito e stampato:
# strato 1, colonna 1, righe 1-n, etc.
array_per_colonne## , , X
##
## D E F G
## A 1 4 7 10
## B 2 5 8 11
## C 3 6 9 12
##
## , , Y
##
## D E F G
## A 13 16 19 22
## B 14 17 20 23
## C 15 18 21 24
##
## , , Z
##
## D E F G
## A 25 28 31 34
## B 26 29 32 35
## C 27 30 33 36# è anche possibile non specificare i nomi
array_senza_nomi <- array(rep(c(1,2,3), each = 6),
dim = c(3,3,2))
array_senza_nomi## , , 1
##
## [,1] [,2] [,3]
## [1,] 1 1 2
## [2,] 1 1 2
## [3,] 1 1 2
##
## , , 2
##
## [,1] [,2] [,3]
## [1,] 2 3 3
## [2,] 2 3 3
## [3,] 2 3 3Nota come sia le matrici che gli array sono vettori che sono conservati in memoria con attributi addizionali (dimensioni, nomi)
as.matrix() e as.array() possono essere usati per trasformare altri oggetti in matrici o array (se possible).
Guarda che succede
## Treatment Sex
## 1 Treated Male
## 2 Treated Male
## 3 Treated Male
## 4 Treated Male
## 5 Treated Male
## 6 Treated Male
## 7 Treated Male
## 8 Treated Male
## 9 Treated Male
## 10 Treated Male## [1] "data.frame"## [1] "matrix" "array"is.matrix() e is.array() possono essere usati per determinare se un oggetto è una matrice o un array.
## [1] FALSE## [1] TRUE## [1] TRUENota che, le matrici, in effetti, sono array.
4.6 I data frame e le liste.
Matrici e array sono oggetti utili, ma il vincolo che debbano contenere valori dello stesso tipo è piuttosto stringente e la loro organizzazione in righe e colonne è, essa stessa, rigida.
Come hai visto nella Premessa 2 (paragrafo 4.1.2) una tabella contiene normalmente variabili di tipo diverso: ogni colonna è, o dovrebbe essere, una variabile, e ogni riga è una singola osservazione; tutte le colonne hanno la stessa lunghezza. In R, questi tipi di oggetti sono chiamati data frame e ne abbiamo già visto diversi esempi (Arthritis, Iris, Billboard).
4.6.1 I data frame, nel bene e nel male.
È possibile creare nuovi data frame in diversi modi:
con il comando
data.frame()convertendo oggetti a 2 dimensioni esistenti (p.es. una matrice) con
as.data.frame()unendo colonne della stessa lunghezza con il comando
cbind()
I pacchetti del tidyverse operano sui data frame e, spesso, operano su oggetti simili ai data frame, le tibbles, con default e proprietà sensibilmente migliorate.93.
I data frame sono oggetti molto flessibili (possono addirittura avere colonne che contengono altri data frame!) e, come vedrai, sono gli oggetti che usiamo più frequentemente per trattare tabelle di dati. In passato (versioni precedenti alla 4.0.0)94 avevano una noiosissima opzione di default che trasformava le colonne di variabili nominali in fattori. Il modo in cui vengono stampati è un tantino ridondante95 e poco informativo.
Le tibbles hanno proprietà migliori. Prova anche la funzione pillar::glimpse(), come modo alternativo per esplorare un data frame o una tibble.
Per saperne di più su data frames e tibbles scrivi nella console:
?data.frame
?tibble::tibbleVediamo un po’ di creare dei data frame.
## rep.1.4..2. rep.1.4..each...2. mantra.1.8.
## 1 1 1 amore
## 2 2 1 pace
## 3 3 2 amore
## 4 4 2 pace
## 5 1 3 amore
## 6 2 3 pace
## 7 3 4 amore
## 8 4 4 paceApprofitta per esplorare il comportamento della funzione rep(). Le colonne hanno nomi? Di che tipo è la terza colonna? Di che tipo era il vettore usato per crearla? Qual’è il default del parametro stringsAsFactors nel comando data.frame()?
Puoi assegnare nomi a righe e colonne dopo la creazione del dataframe:
# assegno nomi alle colonne:
colnames(data_frame_4) <- c("quattro","quattro_coppie","mantra")
data_frame_4## quattro quattro_coppie mantra
## 1 1 1 amore
## 2 2 1 pace
## 3 3 2 amore
## 4 4 2 pace
## 5 1 3 amore
## 6 2 3 pace
## 7 3 4 amore
## 8 4 4 paceNota come:
ho usato un vettore per assegnare nomi;
se tu avessi fatto girare i comandi in R un oggetto di nome
mantraesisterebbe ora come oggetto isolato e come colonna del data frame
Quali sono i nomi delle righe? Possiamo assegnarli?
## [1] "1" "2" "3" "4" "5" "6" "7" "8"## quattro quattro_coppie mantra
## a 1 1 amore
## b 2 1 pace
## c 3 2 amore
## d 4 2 pace
## e 1 3 amore
## f 2 3 pace
## g 3 4 amore
## h 4 4 paceNota la costante letters e la funzione nrow().
Puoi creare un data frame convertendo una matrice:
O puoi usare cbind, che unisce per colonne
## D E F D E F
## A 1 4 7 1 4 7
## B 2 5 8 2 5 8
## C 3 6 9 3 6 9O rbind che unisce per righe
## D E F
## A 1 4 7
## B 2 5 8
## C 3 6 9
## A1 1 4 7
## B1 2 5 8
## C1 3 6 9Quando si uniscono molti data frame o data frame di grandi dimensioni si possono usare i comandi equivalenti di dplyr. Prova a eseguire i seguenti comandi nella console:
molta_artrite <- dplyr::bind_rows(Arthritis, Arthritis)
sei_per_tre <- dplyr::bind_cols(tre_per_tre, tre_per_tre)Ricordati che puoi omettere dplyr:: se non c’è ambiguità nel nome della funzione mentre non puoi farlo se una funzione con lo stesso nome lo ha “mascherato” durante il caricamento dei pacchetti; nota come i nomi delle due funzioni bind_rows() e bind_cols() siano più intuitivi di rbind() e cbind(): questa è una caratteristica di molte funzioni e parametri di funzioni del tidyverse.
Le tibbles sono una versione “migliorata” dei data frame. Le puoi creare trasformando un data frame on con il comando tibble():
## # A tibble: 84 × 5
## ID Treatment Sex Age Improved
## <int> <fct> <fct> <int> <ord>
## 1 57 Treated Male 27 Some
## 2 46 Treated Male 29 None
## 3 77 Treated Male 30 None
## 4 17 Treated Male 32 Marked
## 5 36 Treated Male 46 Marked
## 6 23 Treated Male 58 Marked
## 7 75 Treated Male 59 None
## 8 39 Treated Male 59 Marked
## 9 33 Treated Male 63 None
## 10 55 Treated Male 63 None
## # ℹ 74 more rows## [1] "tbl_df" "tbl" "data.frame"Nota che il modo in cui viene stampata una tibble è diverso e prende meno spazio in console. Le tibbles mantengono la classe data.frame.
Puoi anche creare una tibble da 0 con il comando tibble, del pacchetto tibble
Se ti va, puoi esplorare il comando tribble() del pacchetto tibble: è un modo semplice per creare piccolissimi data frame scrivendoli in modo più naturale, per righe invece che per colonne.
Un’ultima cosa: in genere è una pessima idea inserire direttamente in formato interattivo un data frame in R. Tecnicamente puoi farlo creando un data frame nullo e invocando l’editor (che è piattaforma-specifico e molto, molto lento).
Prova ad eseguire questo script:
df <- data.frame(NULL)
# ci vuole un po' per aprire l'editor
df <- edit(df)Sostituendo df con un nome di un data frame esistente puoi editarlo manualmente.
4.6.2 Le liste.
Le liste sono gli oggetti più flessibili in R. Possono contenere tipi di oggetti diversi e non ci sono vincoli al tipo e alla lunghezza (tranne, suppongo, la memoria). Sono importanti perché sono gli oggetti che molte funzioni statistiche restituiscono come risultati.96
Il comando per creare una lista è, abbastanza prevedibilmente, list(). Se hai tempo, esplora l’aiuto.
# creiamo la nostra prima lista
la_mia_prima_lista <- list(b, due_vettori, mantra, per_colonne)
# nota in che modo viene stampata;
la_mia_prima_lista## [[1]]
## [1] 1 2 3
##
## [[2]]
## [1] "1" "2" "3" "1" "2" "3" "d" "e" "f"
##
## [[3]]
## [1] "amore" "pace" "amore" "pace" "amore" "pace" "amore" "pace" "amore"
## [10] "pace" "amore" "pace"
##
## [[4]]
## D E F
## A 1 4 7
## B 2 5 8
## C 3 6 9## List of 4
## $ : num [1:3] 1 2 3
## $ : chr [1:9] "1" "2" "3" "1" ...
## $ : chr [1:12] "amore" "pace" "amore" "pace" ...
## $ : int [1:3, 1:3] 1 2 3 4 5 6 7 8 9
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : chr [1:3] "A" "B" "C"
## .. ..$ : chr [1:3] "D" "E" "F"## [1] TRUE## [1] TRUE# le liste possono avere nomi, e possono essere annidate, cioé contenere altre liste
la_mia_prima_lista_con_nomi <- list(a = b,
b = due_vettori,
c = mantra,
d = per_colonne,
e = la_mia_prima_lista)
str(la_mia_prima_lista_con_nomi)## List of 5
## $ a: num [1:3] 1 2 3
## $ b: chr [1:9] "1" "2" "3" "1" ...
## $ c: chr [1:12] "amore" "pace" "amore" "pace" ...
## $ d: int [1:3, 1:3] 1 2 3 4 5 6 7 8 9
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : chr [1:3] "A" "B" "C"
## .. ..$ : chr [1:3] "D" "E" "F"
## $ e:List of 4
## ..$ : num [1:3] 1 2 3
## ..$ : chr [1:9] "1" "2" "3" "1" ...
## ..$ : chr [1:12] "amore" "pace" "amore" "pace" ...
## ..$ : int [1:3, 1:3] 1 2 3 4 5 6 7 8 9
## .. ..- attr(*, "dimnames")=List of 2
## .. .. ..$ : chr [1:3] "A" "B" "C"
## .. .. ..$ : chr [1:3] "D" "E" "F"Vedremo dopo il significato di [[]].
Imparare ad usare le liste è molto importante e dovresti esercitarti nella loro creazione e sul modo in cui si selezionano ed estraggono elementi dalle liste (4.8).
4.7 Altre cose strane: tabelle di conte, serie temporali, date e ore.
Ci sono alcuni altre strutture di dati che hanno proprietà speciali: potrebbero servirti, ma, se hai fretta puoi saltare questo paragrafo.
In particolare, R ha classi particolari per:
le tabelle di conte: si ottengono come risultato della funzione
table(), che restituisce tabelle di frequenza o di contingenza (vettori, matrici e array) di numeri interi, derivati dalle conte dell’occorrenza di combinazioni di variabili quantitativele serie temporali: si creano con la funzione
ts()e contenogno solo i valori e l’indicazione della frequenza (annuale, mensile, etc.)gli oggetti di tipo data (
date) e data/tempo (date-time) sono particolarmente importanti, sia perché richiedono la possibilità di stampa in formati diversi, sia perché i fusi orari possono introdurre delle complicazioni nel confronto delle ore97
Prova a esplorare l’aiuto sulle funzioni scrivendo (o copiando e incollando) nella tua console:
?table
?ts
?DateTimeClasses
?as.DateOppure studia questi semplici esempi:
# Tabelle
# ecco una tabella che conta il numero di casi con nessun miglioramento (None)
# qualche miglioramento (Some) e un deciso miglioramento (Marked),
# in funzione del trattamento (Placebo o Treated) e del sesso
tabella_artrite <- table(Arthritis$Treatment, Arthritis$Improved, Arthritis$Sex)
tabella_artrite## , , = Female
##
##
## None Some Marked
## Placebo 19 7 6
## Treated 6 5 16
##
## , , = Male
##
##
## None Some Marked
## Placebo 10 0 1
## Treated 7 2 5## [1] "table"## [1] TRUE## [1] TRUELe serie temporali (time series) sono importanti in molti campi, ma specialmente in economia. R ha oggetti speciali per le serie temporali, che sono generati dalla funzione ts().
# un oggetto di classe time series:
data("AirPassengers")
# sono i totali, in migliaia, dei passaggeri delle linee aeree mondiali dal 1949 al 1960, per mese
AirPassengers## Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 1949 112 118 132 129 121 135 148 148 136 119 104 118
## 1950 115 126 141 135 125 149 170 170 158 133 114 140
## 1951 145 150 178 163 172 178 199 199 184 162 146 166
## 1952 171 180 193 181 183 218 230 242 209 191 172 194
## 1953 196 196 236 235 229 243 264 272 237 211 180 201
## 1954 204 188 235 227 234 264 302 293 259 229 203 229
## 1955 242 233 267 269 270 315 364 347 312 274 237 278
## 1956 284 277 317 313 318 374 413 405 355 306 271 306
## 1957 315 301 356 348 355 422 465 467 404 347 305 336
## 1958 340 318 362 348 363 435 491 505 404 359 310 337
## 1959 360 342 406 396 420 472 548 559 463 407 362 405
## 1960 417 391 419 461 472 535 622 606 508 461 390 432# nota come sia formattato come una matrice
# creiamo una serie fittizia con frequenza annuale
i_miei_anni <-ts(1:50, start = 1960, frequency = 1)
# per frequency 1 rappresenta gli anni, 4 i trimestri, 12 i mesi,
# 6 groups di 10 minuti in un'ora, 7 i giorni, 24 le ore in un giorno
# 30 i mesi in un anno
print(i_miei_anni)## Time Series:
## Start = 1960
## End = 2009
## Frequency = 1
## [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
## [26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50# ora una serie mensile, dal 1960 al 1968
(i_miei_mesi <- ts(c(1:50,50:1), start = c(1960,2), frequency = 12))## Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 1960 1 2 3 4 5 6 7 8 9 10 11
## 1961 12 13 14 15 16 17 18 19 20 21 22 23
## 1962 24 25 26 27 28 29 30 31 32 33 34 35
## 1963 36 37 38 39 40 41 42 43 44 45 46 47
## 1964 48 49 50 50 49 48 47 46 45 44 43 42
## 1965 41 40 39 38 37 36 35 34 33 32 31 30
## 1966 29 28 27 26 25 24 23 22 21 20 19 18
## 1967 17 16 15 14 13 12 11 10 9 8 7 6
## 1968 5 4 3 2 1# un calendario settimanale, che parte dal 12° giorno della 12° settimana
i_miei_giorni <- ts(c(1:7,7:1,1:7,7:1), start = c(12,2), frequency = 7)
print(i_miei_giorni, calendar = T)## p1 p2 p3 p4 p5 p6 p7
## 12 1 2 3 4 5 6
## 13 7 7 6 5 4 3 2
## 14 1 1 2 3 4 5 6
## 15 7 7 6 5 4 3 2
## 16 1Anche gli oggetti di tempo e data hanno comandi dedicati. Ecco per esempio un vettore di variabili di tipo carattere, nel formato di default per le date: anno, mese, giorno
## [1] "character"le_mie_date_sbagliate <- c("14/02/1962","07/12/1964")
# convertiamo in date
le_mie_Date <- as.Date(le_mie_date)
typeof(le_mie_Date)## [1] "double"## [1] -2878 -1851Nota come si tratti di interi: il numero di giorni dal 1/1/1970 (negativi se la data è precedente). Fornendo a R la formattazione corretta è possibile convertire diversi formati
## [1] "1962-02-14" "1964-12-07"Esplora l’aiuto di as.Date per i diversi codici di formattazione. Ovviamente il formato si può cambiare:
le_mie_Date_formattate <- format(le_mie_Date_formattate, format = "%A %d %B %y")
le_mie_Date_formattate## [1] "Wednesday 14 February 62" "Monday 07 December 64"## [1] "Wednesday 14 February 62" "Monday 07 December 64 "## [1] "Wednesday 14 February 62" "Monday 07 December 64"Ci sono funzioni speciali per ottenere l’ora e la data di sistema e si possono fare operazioni su date:
Si possono calcolare differenze fra date, in diverse unità. Scrivi questo nella console:
>?difftime## Time difference of 146.7143 weeksSe vuoi saperne di più sui formati di data e tempo leggi Advanced R o la vignetta per il pacchetto lubridate.
4.8 Indirizzare, selezionare.
Un’attività fondamentale in R è quella di selezionare singoli elementi o gruppi di elementi appartenenti ad oggetti più complessi, in modo da poterli visualizzare, utilizzare come input in altri comandi, o cambiarne il valore.
Anche se nel capitolo 9 vedremo alcuni comandi piuttosto intuitivi usati per estrarre colonne, righe o sottoinsiemi da un data frame o una tibble, è indispensabile conoscere gli operatori di base, come [], [[]] e $.
4.8.1 Indirizzare per posizione.
Per tutti i tipi di vettori di R è possibile indirizzare singoli elementi per posizione usando [].
Ogni elemento di un vettore ha un indice e in R gli indici partono da 1 (l’ho già detto?). Nei vettori a una dimensione sarà possibile indirizzare un singolo elemento indicandone la posizione, o gruppi di elementi usando una sequenza o un vettore di posizioni, adiacenti o non adiacenti. Nei vettori a 2 o più dimensioni (matrici, array, data frame) è possibile indirizzare singole posizioni (usando gli indici del singolo elemento per tutte le dimensioni) o gruppi di elementi appartenenti a diverse righe, colonne, strati.
## [1] "1" "2" "3" "1" "2" "3" "d" "e" "f"## [1] "3"## [1] "1" "2" "3"## [1] "3" "2" "1"## [1] "1" "2" "1" "d"# naturalmente possiamo usare queste espressioni per assegnare l'oggetto
# risultante a un nome
quattro_elementi <- due_vettori[c(1,2,4,7)]
# ripetere l'indice di una posizione è l'equivalente di duplicare o
# triplicare l'elemento nel vettore che ne risulta
due_vettori[c(1,1,1,2,2,2)]## [1] "1" "1" "1" "2" "2" "2"# possiamo usare gli indici per cambiare singoli elementi o elementi multipli
# di un vettore esistente
a## [1] 1 2 3## [1] 1 2 4## [1] 3 2 1Ovviamente, indirizzare e selezionare in oggetti a due o più dimensioni è più complesso, ma abbastanza intuitivo. In un oggetto a due dimensioni, come una matrice o un data frame, se usiamo un solo indice indirizziamo le colonne.
## D E F
## A 1 4 7
## B 2 5 8
## C 3 6 9## E
## A 4
## B 5
## C 6## D E
## A 1 4
## B 2 5
## C 3 6Per indirizzare le righe possiamo usare la notazione [n,]: “,” seleziona tutte le colonne o, analogamente, tutte le righe:
## D E F
## B 2 5 8## [1] 4 5 6Possiamo indirizzare un singolo elemento usando entrambi gli indici, di riga e colonna o indirizzare un gruppo di elementi, adiacenti o meno, usando vettori di posizioni:
## [1] 1## D E
## A 1 4
## B 2 5## D F
## A 1 7
## C 3 9Vale quanto detto in precedenza: possiamo usare questa procedura per attribuire gli oggetti risultanti ad altri nomi o per assegnare nuovi valori a elementi singoli o multipli:
## D F
## A 1 7
## C 3 9## D F
## A 2 7
## C 3 9## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 5.1 3.5 1.4 0.2 setosa
## 2 4.9 3.0 1.4 0.2 setosa
## 3 4.7 3.2 1.3 0.2 setosa
## 4 4.6 3.1 1.5 0.2 setosa
## 5 5.0 3.6 1.4 0.2 setosaPrincipi analoghi valgono per gli array:
## , , 1
##
## [,1] [,2] [,3]
## [1,] 1 1 2
## [2,] 1 1 2
## [3,] 1 1 2
##
## , , 2
##
## [,1] [,2] [,3]
## [1,] 2 3 3
## [2,] 2 3 3
## [3,] 2 3 3## [1] 1# un vettore composto dalle prime tre righe della 2° colonna del 2° strato
array_senza_nomi[1:3,2,2]## [1] 3 3 3## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 5.1 3.5 1.4 0.2 setosa## [1] 1 1 1## [1] 1 3Anche per le liste (e per le liste annidate) è possibile usare l’indirizzamento per posizione con [], ma gli elementi vengono estratti come liste. Per estrarre un elemento di una lista con la sua classe di origine è necessario usare l’operatore [[]]. E’ importante ricordare bene l’uso di [] e [[]] per le liste, perché altrimenti si possono ottenere risultati erronei o inattesi.
Infine, per i vettori atomici a più di una dimensione (matrici e array), bisogna fornire indici per tutte le dimensioni. Che succede se usi una sola dimensione? prova da solo con array_senza_nomi.
## $a
## [1] 1 2 3
##
## $b
## [1] "1" "2" "3" "1" "2" "3" "d" "e" "f"
##
## $c
## [1] "amore" "pace" "amore" "pace" "amore" "pace" "amore" "pace" "amore"
## [10] "pace" "amore" "pace"
##
## $d
## D E F
## A 1 4 7
## B 2 5 8
## C 3 6 9
##
## $e
## $e[[1]]
## [1] 1 2 3
##
## $e[[2]]
## [1] "1" "2" "3" "1" "2" "3" "d" "e" "f"
##
## $e[[3]]
## [1] "amore" "pace" "amore" "pace" "amore" "pace" "amore" "pace" "amore"
## [10] "pace" "amore" "pace"
##
## $e[[4]]
## D E F
## A 1 4 7
## B 2 5 8
## C 3 6 9## $a
## [1] 1 2 3## [1] "list"## [1] 1 2 3## [1] "numeric"# un elemento di un elemento
# come lista
# prima troviamo la lunghezza della lista
length(la_mia_prima_lista_con_nomi)## [1] 5# il quinto elemento, oltre ad essere un bel film, è una lista,
# il cui 4° elemento è una matrice
la_mia_prima_lista_con_nomi[[5]][[4]]## D E F
## A 1 4 7
## B 2 5 8
## C 3 6 9## A B C
## 1 2 3# questo funziona, e calcola la somma degli elementi del primo vettore
sum(la_mia_prima_lista_con_nomi[[1]])## [1] 6Questo invece non funzionerebbe, prova a scrivrlo nella console:
>sum(la_mia_prima_lista_con_nomi[1])4.8.2 Usare i nomi.
I nomi98 sono attributi particolarmente importanti per le operazioni di indirizzamento e di filtraggio.
L’operatore $ permette di indirizzare per nome le colonne (in data frame e tibble99) o gli elementi (nelle liste)100. E’ importante ricordare due proprietà di questo operatore:
se usato per le colonne di data frame o tibble
$, se non c’è ambiguità funziona anche con corrispondenze parziali101nelle liste estrae gli elementi con la loro classe originale
E’ possibile combinare l’indirizzamento con $ con quello con [].
## [1] Some None None Marked Marked
## Levels: None < Some < Marked## [1] Marked Marked None None Some
## Levels: None < Some < Marked## [1] "ID" "Treatment" "Sex" "Age" "Improved"Che succede se uso solo la A? Dal momento che viene trovata anche una corrispondenza parziale, restituirà Age (per brevità uso head() per ottenere solo i primi elementi):
## [1] 27 29 30 32 46 58## [1] 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5## NULLNelle liste $ estrae l’elemento con la sua classe originale. Proviamo innanzitutto a dare nomi a elementi dell’elemento e della lista la_mia_prima_lista_con_nomi
names(la_mia_prima_lista_con_nomi$e) <- c("aa", "ab", "ac", "ad")
# e ora vediamo che succede
la_mia_prima_lista_con_nomi$a## [1] 1 2 3## [1] "numeric"## $aa
## [1] 1 2 3
##
## $ab
## [1] "1" "2" "3" "1" "2" "3" "d" "e" "f"
##
## $ac
## [1] "amore" "pace" "amore" "pace" "amore" "pace" "amore" "pace" "amore"
## [10] "pace" "amore" "pace"
##
## $ad
## D E F
## A 1 4 7
## B 2 5 8
## C 3 6 9## [1] "list"## [1] 1 2 34.8.3 Usare valori logici.
Infine, il modo forse più flessibile per indirizzare elementi è quello di usare valori logici, sia come il risultato di operazioni e confronti, che come vettori o matrici logiche.
Alcuni esempi chiariranno meglio il concetto. Per queste operazioni sono molto utili:
l’operatore
%in%che permettono di trovare corrispondenze di un vettore in un altro, restituendo un vettore logicola funzione
which()che restituisce un vettore delle posizioni con valoreTin un vettore logicola funzione
subset()che permette di estrarre elementi da vettori, matrici o data frame sulla base di condizioni logiche
Per selezionare, attribuire o sostituire elementi è possibile usare vettori logici creati per l’occasione o ottenuti come risultato di altre funzioni:
tre_selezioni <- c(T,F,T)
# estrae il 1° e terzo elemento da vettore_con_nomi e li
# attribuisce a un altro vettore
due_elementi <- vettore_con_nomi[tre_selezioni]Naturalmente è possibile fare lo stesso con matrici: prova a capire cosa succede negli esempi successivi.
## D E F
## A 1 4 7
## B 2 5 8
## C 3 6 9## [1] 1 2 4 5 7 8## D E F
## A FALSE TRUE TRUE
## B FALSE TRUE TRUE
## C FALSE TRUE TRUE## [1] 4 5 6 7 8 9## [1] 4 5 6 7 8 9## [1] 4 5 6 7 8 9## [1] "ID" "Treatment" "Sex" "Age" "Improved"## [1] TRUE FALSE FALSE FALSE FALSE# che vettore restituisce l'espressione precedente?
# individuare le posizioni di due colonne in Arthritis sulla base dei nomi
# nota l'uso dell'operatore |, che rappresenta un OR logico,
# sono selezionate le condizioni per cui è vera l'una o l'altra espressione
colnames(Arthritis) == "ID" | colnames(Arthritis) == "Age" ## [1] TRUE FALSE FALSE TRUE FALSE# oppure potrei usare %in%
# creo un vettore dei nomi che voglio cercare
i_nomi <- c("ID","Age")
colnames(Arthritis) %in% i_nomi ## [1] TRUE FALSE FALSE TRUE FALSE## [1] 1 4## ID Age
## 1 57 27
## 2 46 29
## 3 77 30
## 4 17 32
## 5 36 46
## 6 23 58La funzione subset() consente invece di filtrare righe sulla base di condizioni logiche e di selezionare opzionalmente solo alcune variabili
## Sex Age Improved
## 13 Male 69 None
## 14 Male 70 Marked
## 37 Female 68 Some
## 38 Female 68 Marked
## 39 Female 69 None
## 40 Female 69 Some
## 41 Female 70 Some
## 83 Female 68 Some
## 84 Female 74 MarkedGli stessi risultati possono essere ottenuti con gli operatori e i metodi descritti prima, ma in maniera decisamente più complessa. Vuoi provarci?
Molte altre utili funzioni per selezionare e estrarre elementi con una sintassi molto più intuitiva sono disponibili in pacchetti del tidyverse, come dplyr, ed avremo modo di parlarne nei capitoli successivi per poi descriverle in maniera più sistematica nel capitolo 9.
4.9 attach(), with(), within().
R è piuttosto pignolo come linguaggio: bisogna indicare specificamente dove cercare l’oggetto su cui eseguire una operazione. Nell’esempio seguente, la colonna Age compare in più di un data frame e, se vogliamo utilizzarla in una funzione, dobbiamo indicare esplicitamente dove si trova. Questo rende molto verbosi i comandi. Alcune funzioni del pacchetto base permettono di aggirare questo problema, che, a dire la verità, è gestito molto meglio nell’insieme dei pacchetti del tidyverse (vedi capitolo 9).
Anche se lo abbiamo già fatto, apriamo il data set Arthritis e creiamone una copia (bisogna aver caricato il pacchetto vcd):
La variabile Age è in entrambi; usare solo il nome di colonna non funzionerebbe, prova tu a inserire nella console:
> head(Age)Per permettere a R di “trovare” Age dobbiamo dire dove cercare:
## [1] 27 29 30 32 46## [1] 48 55 55 56 57Questo rende i comandi “verbosi”. Qui cerco i valori di Age per Sex == “Female”
## [1] 23 32 37 41 41 48Naturalmente questi valori sarebbero diversi per Arthr2
## [1] 48 55 55 56 57 57 57 58 59 59 60 61 62 62 66 67 68 68 69 69attach() semplifica alcune di queste operazioni; tuttavia, per evitare ambiguità, è sempre opportuno usare detach() per “staccare” l’oggetto dal percorso di ricerca:
## [1] Treated Treated Treated Treated Treated
## Levels: Placebo Treated## Placebo Treated
## 0 20## [1] 48 55 55 56 57 57 57 58 59 59 60 61 62 62 66 67 68 68 69 69La funzione summary() fornisce alcune statistiche riassuntive per un oggetto; le statistiche variano con il tipo di variabile.
In alternativa è possibile usare with()
## [1] 955Gli oggetti creati all’interno di with() non sono disponibili nel global environment; per questo bisogna usare il comando <<- per l’assegnazione
print(somma_età) restituirebbe un errore mentre questi due comandi funzionano:
## [1] 9554.10 Funzioni “built-in” e funzioni definite dall’utente.
In R tutto quello che accade, accade perché hai invocato una funzione: lo ho già detto, no? Abbiamo già visto moltissime funzioni e moltissime altre ne incontrerai nella tua carriera di programmatore.
Se vuoi puoi saltare questo paragrafo: in fondo, puoi imparare le funzioni “sul campo”, usandole man mano che ti servono. Tuttavia, è bene mettere alcuni punti fermi.
4.10.1 Semplici funzioni matematiche, trigonometriche, statistiche, logiche, etc.
R base ha moltissime funzioni matematiche, statistiche, logiche e molte altre sono aggiunte dai pacchetti contribuiti da utenti. Qui ne richiamerò solo alcune, aggiungendo qualche altro piccolo elemento sulla priorità delle operazioni, etc., giusto nel caso tu non abbia mai avuto nessuna esperienza di programmazione. Per maggiori informazioni sugli operatori puoi visitare questa pagina, mentre per le funzioni più comuni puoi visitare questa.
4.10.2 Operatori.
Gli operatori matematici e logici in R non sono molto diversi da quelli che si usano in altri linguaggi, o, se per questo, nelle formule dei più comuni fogli di calcolo.
Operatori matematici
| Operatore | Cosa fa? | Uso |
|---|---|---|
| + | addizione | 1 + 2 |
| - | sottrazione | 2 - 1 |
| * | moltiplicazione | 3 * 1 |
| / | divisione | 4 / 2 |
| ^ o ** | elevazione a potenza | 2^2 |
| x%%y | modulo | 7%%3 (=1) |
| x%/%y | divisione intera | 7%/%3 (=2) |
Gli operatori matematici sono, a tutti gli effetti, delle funzioni102. Ricorda che puoi usare la console come se fosse una calcolatrice: prova a scrivere nella console il seguente codice (ricorda di rimuovere il prompt e premere invio alla fine di ogni riga):
>1+2
>2^5
>7%%2
>5/0
>0/0La priorità delle operazioni è quella solita (^,/ e *, + e -) e, per modificarla, occorre usare le parentesi tonde. Inoltre in R le operazioni sono vettorializzate. Guarda questi semplici esempi per capire meglio il funzionamento degli operatori matematici.
## [1] 3## [1] 2.5# le operazioni sono vettorializzate; guarda che succede se aggiungo
# uno scalare a un vettore o se moltiplico uno scalare per un vettore
y <- c(1,2,3,4)
(y+1)## [1] 2 3 4 5## [1] 1.1 2.2 3.3 4.4## [1] 0.5 1.0 1.5 2.0 NA# nelle operazioni fra vettori, il vettore più corto viene riciclato,
# se necessario con un warning
w <- c(1,2) # è un vettore di lunghezza inferiore a y
length(w) < length(y)## [1] TRUE## [1] 1 2## [1] 1 2 3 4## [1] 2 4 4 6## Warning in y + k: longer object length is not a multiple of shorter object
## length## [1] 2 4 6 5Nota che le operazioni a virgola mobile potrebbero dare risultati sorprendenti: quindi (sqrt(2))^2==2 è falso; la funzione near()di dplyrserve proprio per affrontare questo problema: dplyr::near((sqrt(2)^2),2).
Nota inoltre che la moltiplicazione fra matrici è un’operazione diversa da quella condotta con l’operatore *: x %*% y. Come probabilmente ricorderai dai corsi di matematica e algebra lineare che hai frequentato perché l’operazione sia possibile il numero di colonne di x deve essere uguale al numero di righe di y; se x è una matrice nxm e y è mxp il risultato è una matrice nxp.
## [,1] [,2] [,3]
## [1,] 1.1 1.2 1.3
## [2,] 2.1 2.2 2.3## [,1] [,2] [,3]
## [1,] 1.15 1.25 1.35
## [2,] 2.15 2.25 2.35## [,1] [,2] [,3]
## [1,] 0.55 0.6 0.65
## [2,] 1.05 1.1 1.15## [,1] [,2] [,3]
## [1,] 1.11 1.23 1.32
## [2,] 2.12 2.21 2.33## [,1] [,2] [,3]
## [1,] 1.20 1.30 1.40
## [2,] 2.15 2.25 2.35La coercizione può dare risultati interessanti. Prova ad eseguire le seguenti operazioni nella console:
>un_logico <- c(T,T,F)
>3*un_logico
>un_fattore <- factor(c("a", "b", "c", "b"))
>3*un_fattore
>3*as.numeric(un_fattore)Come ti spieghi i risultati?
Operatori logici.
L’uso di operatori logici è molto frequente in R. Gli operatori logici, prevedibilmente, restituiscono vettori di valori logici (che sono equivalenti agli interi 1 per TRUE e 0 per FALSE).
| Operatore | Description | Esempio |
|---|---|---|
| < | minore di | 5 < 4 è FALSE |
| > | maggiore di | 5 > 4 è TRUE |
| <= | minore o uguale a | 5 <= 5 è TRUE |
| >= | maggiore o uguale a | 5 >= 4 è TRUE |
| == | esattamente uguale a | 2 == 2 è TRUE |
| != | diverso da | 2 != 2 è FALSE |
| !x | non x | !(2 != 2) è TRUE |
| x | y | x OR y |
| x & y | x AND y | (5<4) |
| isTRUE(x) | verifica se X è TRUE | isTRUE(5<=5) è TRUE |
Gli operatori logici sono abbastanza semplici da usare e da comprendere e possono essere combinati in vari modi soprattutto per filtrare i dati (vedi capitolo 9). Se vuoi vedere una rappresentazione grafica del loro funzionamento guarda qui.
4.10.3 Funzioni built-in.
R base fornisce numerosissime funzioni matematiche, trigonometriche e statistiche, oltre a funzioni che operano su caratteri. La lista è decisamente troppo lunga per citarla qui. Mi limiterò a presentare alcuni semplici esempi.
Per una lista (più o meno) completa guarda qui.
Ricorda che ogni funzione è caratterizzata da un nome e da una serie di argomenti, e può restituire un valore o avere un effetto collaterale (la stampa di qualcosa nella console, il salvataggio di un file).
Molte funzioni prendono vettori o scalari come input; ecco come si calcola la radice quadrata
## [1] 1 2 3Nota che l’argomento di una funzione può essere un’altra funzione, come in effetti accade nella riga precedente: c() è essa stessa una funzione.
Il calcolo del logaritmo neperiano (attent* agli errori!, possono bloccare il flusso di uno script):
## [1] 2.302585Logaritmo in base 10 di e
## [1] 0.4342945Un modo per “intrappolare” un errore:
## Warning in log(-1): NaNs produced## [1] NaNCerca try() e tryCatch() nell’aiuto.
Alcune funzioni che prendono vettori come input
## [1] 4482## [1] 53.35714Alcune funzioni restituiscono un vettore di valori, come il calcolo del range, o la statistica a 5 numeri di Tukey (minimum, lower-hinge, median, upper-hinge, maximum: lower hing e upper hinge corrispondono al primo e terzo quartile)
## [1] 23 74## [1] 23 46 57 63 74Ecco un po’ di esempi di funzioni che operano su caratteri:
# incollare più valori di testo, con uno spaziatore
paste("questo", "capitolo", "è un po' lungo", sep =" ")## [1] "questo capitolo è un po' lungo"# trovare gli elementi di un vettore che contengono una lettera
# o un pattern di caratteri
# la lettera e in qualsiasi posizione
grep("e", c("Teresa","Mario","Adele"))## [1] 1 3## [1] 3# restituire un valore logico che indica se un pattern è presente in
# un vettore
grepl("e", c("Teresa","Mario","Adele"))## [1] TRUE FALSE TRUELe funzioni base di R che si applicano a vettori di caratteri sono decisamente scomode da ricordare e da usare. Il pacchetto stringr del tidyverse è decisamente migliore (vedi capitolo 9).
Per lavorare bene con le stringhe è opportuno imparare almeno qualcosa delle “espressioni regolari” (regex, regular expression): sono un modo conciso e flessibile per individuare insiemi di caratteri in una stringa. Potete trovare delle buone introduzioni in “R for data science” e in questa vignetta.
Infine attent* a come scrivi il codice: R in effetti si legge dall’interno verso l’esterno e da destra a sinistra e questo può creare confusione. Guarda che succede in questo chunk di codice, che attribuisce ad un oggetto la media del logaritmo dei valori della variabile Arthritis$Age:
## [1] 1.712026# meno sintetico ma più facile da leggere
logAge <- log10(Arthritis$Age)
media_log_age <- mean(logAge)
media_log_age## [1] 1.7120264.10.4 Funzioni definite dall’utente.
Le funzioni definite dall’utente sono molto importanti nella scrittura di codice in R: permettono di semplificare operazioni, renderle più efficienti e flessibili e meno soggette ad errore.
Le funzioni vengono create con il comando function() ed è possibile assegnare (o meno) un nome ad una funzione. Come le funzioni di R e le funzioni disponibili nei pacchetti, le funzioni possono avere un certo numero di parametri opzionali, con dei valori di default.
Quello che segue è un semplice esempio di funzione che restituisce media (eventualmente una media sfrondata o trimmed mean) e deviazione standard o, in alternativa, mediana e deviazione assoluta mediana. Le prime due misure sono più adatte a variabili quantitative continue con una distribuzione che si approssima a quella normale, le altre due a distribuzioni che si discostano significativamente da quella normale e che presentano valori estremi. Se non ricordi cosa sono queste statistiche guarda l’aiuto delle funzioni e consulta un libro di statistica.
stat_descrittive <- function(x, parametriche=TRUE, stampa=FALSE, trm = 0.05, narm = T) {
if (parametriche) {
valore_centrale <- mean(x, trim = trm, na.rm = narm)
dispersione <- sd(x, na.rm = narm)
} else {
valore_centrale <- median(x, na.rm = narm)
dispersione <- mad(x, na.rm = narm)
}
if (stampa & parametriche) {
cat("Media=", valore_centrale, "\n", "SD=", dispersione, "\n")
} else if (stampa & !parametriche) {
cat("Median=", valore_centrale, "\n", "MAD=", dispersione, "\n")
}
risultato <- c(valore_centrale, dispersione)
if (parametriche){
names(risultato) <- c("media","SD")
} else {
names(risultato) <- c("mediana","MAD")
}
return(risultato)
}
stat_età <- stat_descrittive(Arthritis$Age)
print(stat_età, digits = 4)## media SD
## 53.91 12.77# non parametriche, con stampa
stat_età <- stat_descrittive(Arthritis$Age, parametriche = F, stampa = T)## Median= 57
## MAD= 10.3782# parametriche, media sfrondata (o trimmed mean, vengono eliminati il 10% dei valori estremi,
# niente stampa)
stat_età <- stat_descrittive(Arthritis$Age, parametriche = T, trm = 0.1)
print(stat_età, digits = 4)## media SD
## 54.44 12.77Prenditi qualche minuto per capire come funziona la funzione prima di leggere il testo che segue il prossimo esempio, che mostra come il codice che sarebbe necessario scrivere senza la funzione sarebbe più verboso.
# voglio calcolare media e deviazione standard su la stessa
# variabile in tre data frame e creare un vettore con nomi con i risultati
stat_età_1 <- c(media = mean(Arthritis$Age, trm = 0.1),
SD = sd(Arthritis$Age))
stat_età_1## media SD
## 53.35714 12.76917## media SD
## 47.75000 12.76917## media SD
## 60.65000 12.76917## media SD
## 54.44118 12.76917## media SD
## 47.87500 15.75094## media SD
## 60.750000 5.705722Bene, la funzione, di default (parametriche = TRUE fra le opzioni), calcola media e deviazione standard per un vettore (che si spera sia numerico, altrimenti la funzione restituirebbe un errore), con una media sfrondata con una soglia di 0.05. Se cambiassimo parametriche = FALSE otterremmo invece mediana e MAD e se indicassimo stampa = TRUE il risultato verrebbe anche mandato in console come testo. La funzione restituisce come risultato un vettore con nomi (anche questi cambiano in funzione dell’opzione parametriche) che può essere assegnato ad un nome. Nota come la funzione faccia uso di strutture di controllo (if … else) che valutano una condizione per scegliere fra uno o più gruppi di comandi alternativi.
E’ chiaramente possibile copiare e incollare il codice
stat_età_1 <- c(media = mean(Arthritis$Age, trm = 0.1),
SD = sd(Arthritis$Age))molte volte e modificarlo per ottenere lo stesso risultato. Questo tuttavia è poco efficiente e soggetto a errori.
Discuteremo meglio dei vantaggi dell’uso delle funzioni nel Capitolo 9.
4.11 Programmare, con stile.
Questo è un libro per pigri e per persone con poca esperienza di programmazione. Per questa ragione ho deciso, molto a malincuore, di spostare tutto il materiale che riguarda più strettamente la programmazione in R nel Capitolo 9. È in quel capitolo che insieme alle tecniche per manipolare (in senso buono, per selezionare, filtrare, trasformare, unire, etc.) i dati (in inglese: data wrangling) tratterò in maniera sistematica dell’uso di strutture come i loop (for, while, repeat), di altre strutture di controllo come if e if ... else e le alternative per “applicare” funzioni a vettori. Come hai già visto, è inevitabile introdurre alcune di queste strutture nel testo: alcune sono piuttosto intuitive, per le altre puoi fare riferimento, quando necessario, al capitolo 9 o alle diverse fonti che ho citato alla fine di questo capitolo.
Spero vivamente che alla fine ti renderai conto che ogni minuto speso a imparare a programmare bene, e soprattutto, a scrivere codice leggibile e riproducibile, è un minuto (o un’ora, o un giorno) ben speso, che ti farà risparmiare molto tempo in futuro.
4.12 Un ambiente affollato.
Bene, in questo capitolo abbiamo creato parecchi oggetti, che sono finiti in quello che si chiama “Global environment”: se stai usando gli script creati per questo libro prova a vedere in quale pannello appaiono i vari oggetti in RStudio man mano che li crei e che succede cliccando sugli oggetti nel pannello Environment. Oltre ad esaminare l’ambiente di lavoro in modo interattivo usando la GUI di RStudio è possibile “interrogare” l’ambiente con delle funzioni.
# elencare gli oggetti nell'ambiente di lavoro e assegnare
# l'elenco ad un oggetto
i_miei_oggetti <- ls()
head(i_miei_oggetti,10)## [1] "a" "a_capo" "AirPassengers"
## [4] "array_per_colonne" "array_senza_nomi" "Arthr"
## [7] "Arthr1" "Arthr2" "Arthritis"
## [10] "b"Per ottenere informazioni sulla struttura di tutti gli oggetti scrivi nella console (l’output è molto lungo)
>ls.str()Il risultato può essere assegnato a una lista di classe ls_str Per ottenere informazioni sugli oggetti che hanno nomi riconducibili ad un determinato pattern è possibile usare delle espressioni regolari:
## AirPassengers : Time-Series [1:144] from 1949 to 1961: 112 118 132 129 121 135 148 148 136 119 ...
## Arthr : 'data.frame': 84 obs. of 5 variables:
## $ ID : int 80 12 29 38 51 54 76 16 69 31 ...
## $ Treatment: Factor w/ 2 levels "Placebo","Treated": 1 1 1 1 1 1 1 1 1 1 ...
## $ Sex : Factor w/ 2 levels "Female","Male": 1 1 1 1 1 1 1 1 1 1 ...
## $ Age : int 23 30 30 32 37 44 45 46 48 49 ...
## $ Improved : Ord.factor w/ 3 levels "None"<"Some"<..: 1 1 1 1 1 1 1 1 1 1 ...
## Arthr1 : 'data.frame': 20 obs. of 5 variables:
## $ ID : int 57 46 77 17 36 23 75 39 33 55 ...
## $ Treatment: Factor w/ 2 levels "Placebo","Treated": 2 2 2 2 2 2 2 2 2 2 ...
## $ Sex : Factor w/ 2 levels "Female","Male": 2 2 2 2 2 2 2 2 2 2 ...
## $ Age : int 27 29 30 32 46 58 59 59 63 63 ...
## $ Improved : Ord.factor w/ 3 levels "None"<"Some"<..: 2 1 1 3 3 3 1 3 1 1 ...
## Arthr2 : 'data.frame': 20 obs. of 5 variables:
## $ ID : int 82 53 79 26 28 60 22 27 2 59 ...
## $ Treatment: Factor w/ 2 levels "Placebo","Treated": 2 2 2 2 2 2 2 2 2 2 ...
## $ Sex : Factor w/ 2 levels "Female","Male": 1 1 1 1 1 1 1 1 1 1 ...
## $ Age : int 48 55 55 56 57 57 57 58 59 59 ...
## $ Improved : Ord.factor w/ 3 levels "None"<"Some"<..: 3 3 3 3 3 3 3 1 3 3 ...
## Arthritis : 'data.frame': 84 obs. of 5 variables:
## $ ID : int 57 46 77 17 36 23 75 39 33 55 ...
## $ Treatment: Factor w/ 2 levels "Placebo","Treated": 2 2 2 2 2 2 2 2 2 2 ...
## $ Sex : Factor w/ 2 levels "Female","Male": 2 2 2 2 2 2 2 2 2 2 ...
## $ Age : int 27 29 30 32 46 58 59 59 63 63 ...
## $ Improved : Ord.factor w/ 3 levels "None"<"Some"<..: 2 1 1 3 3 3 1 3 1 1 ...## a : num [1:3] 3 2 1
## a_capo : chr "A\nB\nC"
## AirPassengers : Time-Series [1:144] from 1949 to 1961: 112 118 132 129 121 135 148 148 136 119 ...
## array_per_colonne : int [1:3, 1:4, 1:3] 1 2 3 4 5 6 7 8 9 10 ...
## array_senza_nomi : num [1:3, 1:3, 1:2] 1 1 1 1 1 1 2 2 2 2 ...
## Arthr : 'data.frame': 84 obs. of 5 variables:
## $ ID : int 80 12 29 38 51 54 76 16 69 31 ...
## $ Treatment: Factor w/ 2 levels "Placebo","Treated": 1 1 1 1 1 1 1 1 1 1 ...
## $ Sex : Factor w/ 2 levels "Female","Male": 1 1 1 1 1 1 1 1 1 1 ...
## $ Age : int 23 30 30 32 37 44 45 46 48 49 ...
## $ Improved : Ord.factor w/ 3 levels "None"<"Some"<..: 1 1 1 1 1 1 1 1 1 1 ...
## Arthr1 : 'data.frame': 20 obs. of 5 variables:
## $ ID : int 57 46 77 17 36 23 75 39 33 55 ...
## $ Treatment: Factor w/ 2 levels "Placebo","Treated": 2 2 2 2 2 2 2 2 2 2 ...
## $ Sex : Factor w/ 2 levels "Female","Male": 2 2 2 2 2 2 2 2 2 2 ...
## $ Age : int 27 29 30 32 46 58 59 59 63 63 ...
## $ Improved : Ord.factor w/ 3 levels "None"<"Some"<..: 2 1 1 3 3 3 1 3 1 1 ...
## Arthr2 : 'data.frame': 20 obs. of 5 variables:
## $ ID : int 82 53 79 26 28 60 22 27 2 59 ...
## $ Treatment: Factor w/ 2 levels "Placebo","Treated": 2 2 2 2 2 2 2 2 2 2 ...
## $ Sex : Factor w/ 2 levels "Female","Male": 1 1 1 1 1 1 1 1 1 1 ...
## $ Age : int 48 55 55 56 57 57 57 58 59 59 ...
## $ Improved : Ord.factor w/ 3 levels "None"<"Some"<..: 3 3 3 3 3 3 3 1 3 3 ...
## Arthritis : 'data.frame': 84 obs. of 5 variables:
## $ ID : int 57 46 77 17 36 23 75 39 33 55 ...
## $ Treatment: Factor w/ 2 levels "Placebo","Treated": 2 2 2 2 2 2 2 2 2 2 ...
## $ Sex : Factor w/ 2 levels "Female","Male": 2 2 2 2 2 2 2 2 2 2 ...
## $ Age : int 27 29 30 32 46 58 59 59 63 63 ...
## $ Improved : Ord.factor w/ 3 levels "None"<"Some"<..: 2 1 1 3 3 3 1 3 1 1 ...
## billboard : tibble [317 × 79] (S3: tbl_df/tbl/data.frame)
## calcola_media : function (vettore_numerico)
## chiamate_multiple : 'difftime' num 0.00333189964294434
## data_frame_4 : 'data.frame': 8 obs. of 3 variables:
## $ quattro : int 1 2 3 4 1 2 3 4
## $ quattro_coppie: int 1 1 2 2 3 3 4 4
## $ mantra : chr "amore" "pace" "amore" "pace" ...
## df_a : 'data.frame': 84 obs. of 2 variables:
## $ Treatment: Factor w/ 2 levels "Placebo","Treated": 2 2 2 2 2 2 2 2 2 2 ...
## $ Sex : Factor w/ 2 levels "Female","Male": 2 2 2 2 2 2 2 2 2 2 ...
## fai_la_somma : function (a = 1, b = 2, c = 3)
## fattore_non_o : Factor w/ 2 levels "consonant","vowel": 2 1 1
## i_miei_anni : Time-Series [1:50] from 1960 to 2009: 1 2 3 4 5 6 7 8 9 10 ...
## la_mia_lista : List of 1
## $ : chr [1:3] "d" "e" "f"
## la_mia_prima_lista : List of 4
## $ : num [1:3] 1 2 3
## $ : chr [1:9] "1" "2" "3" "1" ...
## $ : chr [1:12] "amore" "pace" "amore" "pace" ...
## $ : int [1:3, 1:3] 1 2 3 4 5 6 7 8 9
## la_mia_prima_lista_con_nomi : List of 5
## $ a: num [1:3] 1 2 3
## $ b: chr [1:9] "1" "2" "3" "1" ...
## $ c: chr [1:12] "amore" "pace" "amore" "pace" ...
## $ d: int [1:3, 1:3] 1 2 3 4 5 6 7 8 9
## $ e:List of 4
## la_mia_tibble : tibble [3 × 2] (S3: tbl_df/tbl/data.frame)
## le_mie_date : chr [1:2] "1962/02/14" "1964/12/07"
## le_mie_Date : Date[1:2], format: "1962-02-14" "1964-12-07"
## le_mie_Date_formattate : chr [1:2] "Wednesday 14 February 62" "Monday 07 December 64"
## le_mie_date_sbagliate : chr [1:2] "14/02/1962" "07/12/1964"
## le_mie_mediane : Named num [1:8] 0.01172 -0.00352 0.00874 0.02158 0.0077 ...
## logAge : num [1:84] 1.43 1.46 1.48 1.51 1.66 ...
## m_a : chr [1:84, 1:2] "Treated" "Treated" "Treated" "Treated" "Treated" ...
## maggiore_di_tre : logi [1:3, 1:3] FALSE FALSE FALSE TRUE TRUE TRUE ...
## mantra : chr [1:12] "amore" "pace" "amore" "pace" "amore" "pace" "amore" "pace" ...
## matrice_carattere : chr [1:3, 1:2] "amore" "amore" "amore" "pace" "pace" "pace"
## matrice_logica : logi [1:3, 1:3] TRUE TRUE TRUE FALSE FALSE FALSE ...
## media_log_age : num 1.71
## mediane : num [1:8] 0.01172 -0.00352 0.00874 0.02158 0.0077 ...
## mediane_apply : Named num [1:8] 0.01172 -0.00352 0.00874 0.02158 0.0077 ...
## mtcars : 'data.frame': 32 obs. of 11 variables:
## $ mpg : num 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
## $ cyl : num 6 6 4 6 8 6 8 4 4 6 ...
## $ disp: num 160 160 108 258 360 ...
## $ hp : num 110 110 93 110 175 105 245 62 95 123 ...
## $ drat: num 3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
## $ wt : num 2.62 2.88 2.32 3.21 3.44 ...
## $ qsec: num 16.5 17 18.6 19.4 17 ...
## $ vs : num 0 0 1 1 0 1 0 1 1 1 ...
## $ am : num 1 1 1 0 0 0 0 0 0 0 ...
## $ gear: num 4 4 4 3 3 3 3 4 4 4 ...
## $ carb: num 4 4 1 1 2 1 4 2 2 4 ...
## n_casi : num 10000
## opar : List of 66
## $ xlog : logi FALSE
## $ ylog : logi FALSE
## $ adj : num 0.5
## $ ann : logi TRUE
## $ ask : logi FALSE
## $ bg : chr "white"
## $ bty : chr "o"
## $ cex : num 1
## $ cex.axis : num 1
## $ cex.lab : num 1
## $ cex.main : num 1.2
## $ cex.sub : num 1
## $ col : chr "black"
## $ col.axis : chr "black"
## $ col.lab : chr "black"
## $ col.main : chr "black"
## $ col.sub : chr "black"
## $ crt : num 0
## $ err : int 0
## $ family : chr ""
## $ fg : chr "black"
## $ fig : num [1:4] 0 1 0 1
## $ fin : num [1:2] 7 5
## $ font : int 1
## $ font.axis: int 1
## $ font.lab : int 1
## $ font.main: int 2
## $ font.sub : int 1
## $ lab : int [1:3] 5 5 7
## $ las : int 0
## $ lend : chr "round"
## $ lheight : num 1
## $ ljoin : chr "round"
## $ lmitre : num 10
## $ lty : chr "solid"
## $ lwd : num 1
## $ mai : num [1:4] 1.02 0.82 0.82 0.42
## $ mar : num [1:4] 5.1 4.1 4.1 2.1
## $ mex : num 1
## $ mfcol : int [1:2] 1 1
## $ mfg : int [1:4] 1 1 1 1
## $ mfrow : int [1:2] 1 1
## $ mgp : num [1:3] 3 1 0
## $ mkh : num 0.001
## $ new : logi FALSE
## $ oma : num [1:4] 0 0 0 0
## $ omd : num [1:4] 0 1 0 1
## $ omi : num [1:4] 0 0 0 0
## $ pch : int 1
## $ pin : num [1:2] 5.76 3.16
## $ plt : num [1:4] 0.117 0.94 0.204 0.836
## $ ps : int 12
## $ pty : chr "m"
## $ smo : num 1
## $ srt : num 0
## $ tck : num NA
## $ tcl : num -0.5
## $ usr : num [1:4] 0 1 0 1
## $ xaxp : num [1:3] 0 1 5
## $ xaxs : chr "r"
## $ xaxt : chr "s"
## $ xpd : logi FALSE
## $ yaxp : num [1:3] 0 1 5
## $ yaxs : chr "r"
## $ yaxt : chr "s"
## $ ylbias : num 0.2
## ora : chr "Sat Nov 25 08:18:09 2023"
## per_colonne_sbagliato : int [1:3, 1:3] 1 2 3 4 5 6 7 8 9
## per_colonne_sbagliato_2 : int [1:3, 1:3] 1 2 3 4 5 6 7 8 1
## play_audio : logi TRUE
## quanto : Factor w/ 4 levels "abbastanza","moltissimo",..: 3 3 4 2 1
## quanto_ord : Ord.factor w/ 4 levels "poco"<"abbastanza"<..: 3 3 1 4 2
## quattro_elementi : chr [1:4] "1" "2" "1" "d"
## risultato : logi [1:3] FALSE FALSE FALSE
## somma_età_2 : int 955
## stat_descrittive : function (x, parametriche = TRUE, stampa = FALSE, trm = 0.05, narm = T)
## stat_età : Named num [1:2] 54.4 12.8
## stat_età_1 : Named num [1:2] 53.4 12.8
## stat_età_2 : Named num [1:2] 47.8 12.8
## stat_età_3 : Named num [1:2] 60.6 12.8
## tabella_artrite : 'table' int [1:2, 1:3, 1:2] 19 6 7 5 6 16 10 7 0 2 ...
## tib_Arthritis : tibble [84 × 5] (S3: tbl_df/tbl/data.frame)
## tre_per_tre_logica : logi [1:3, 1:3] TRUE TRUE FALSE TRUE TRUE FALSE ...
## una_matrice : num [1:2, 1:3] 1.1 2.1 1.2 2.2 1.3 2.3
## una_nuova_matrice : num [1:2, 1:3] 1.11 2.12 1.23 2.21 1.32 2.33
## uso_apply : 'difftime' num 0.0037989616394043
## vettori_concatenati : num [1:6] 1 2 3 1 2 3
## virgolettato : chr [1:3] "'A'" "'B'" "'C'"
## virgolettato_doppio : chr [1:3] "\"A\"" "\"B\"" "\"C\""## array_senza_nomi : num [1:3, 1:3, 1:2] 1 1 1 1 1 1 2 2 2 2 ...
## dimmi_di_si : chr [1:3, 1:3] "Yes" "Yes" "Yes" "Yes" "Yes" "Yes" "Yes" "Yes" "Yes"
## due_elementi : Named num [1:2] 1 3
## due_vettori : chr [1:9] "1" "2" "3" "1" "2" "3" "d" "e" "f"
## espliciti : 'data.frame': 4 obs. of 2 variables:
## $ anno : num 1999 2000 2001 2002
## $ vendite: num 100 NA 101 102
## i : int 8
## i_miei_anni : Time-Series [1:50] from 1960 to 2009: 1 2 3 4 5 6 7 8 9 10 ...
## i_miei_giorni : Time-Series [1:28] from 12.1 to 16: 1 2 3 4 5 6 7 7 6 5 ...
## i_miei_mesi : Time-Series [1:100] from 1960 to 1968: 1 2 3 4 5 6 7 8 9 10 ...
## i_miei_oggetti : chr [1:106] "a" "a_capo" "AirPassengers" "array_per_colonne" ...
## i_nomi : chr [1:2] "ID" "Age"
## impliciti : 'data.frame': 3 obs. of 2 variables:
## $ anno : num 1999 2001 2002
## $ vendite: num 100 101 102
## la_mia_prima_lista_con_nomi : List of 5
## $ a: num [1:3] 1 2 3
## $ b: chr [1:9] "1" "2" "3" "1" ...
## $ c: chr [1:12] "amore" "pace" "amore" "pace" ...
## $ d: int [1:3, 1:3] 1 2 3 4 5 6 7 8 9
## $ e:List of 4
## n_casi : num 10000
## oggi : POSIXct[1:1], format: "2023-11-25 08:18:09"
## quattro_elementi : chr [1:4] "1" "2" "1" "d"
## tempi : 'difftime' Named num [1:4] 0.00333189964294434 0.00661516189575195 0.0037989616394043 0.00310111045837402
## tre_per_sei : 'data.frame': 3 obs. of 6 variables:
## $ D: int 1 2 3
## $ E: int 4 5 6
## $ F: int 7 8 9
## $ D: int 1 2 3
## $ E: int 4 5 6
## $ F: int 7 8 9
## tre_selezioni : logi [1:3] TRUE FALSE TRUE
## vettore_con_nomi : Named num [1:3] 1 2 3
## vettori_concatenati : num [1:6] 1 2 3 1 2 3## per_colonne : int [1:3, 1:3] 1 2 3 4 5 6 7 8 9
## per_colonne_sbagliato : int [1:3, 1:3] 1 2 3 4 5 6 7 8 9
## per_colonne_sbagliato_2 : int [1:3, 1:3] 1 2 3 4 5 6 7 8 1
## per_righe : int [1:3, 1:3] 1 4 7 2 5 8 3 6 9## maggiore_di_tre : logi [1:3, 1:3] FALSE FALSE FALSE TRUE TRUE TRUE ...
## sei_per_tre : 'data.frame': 6 obs. of 3 variables:
## $ D: int 1 2 3 1 2 3
## $ E: int 4 5 6 4 5 6
## $ F: int 7 8 9 7 8 9
## tre_per_sei : 'data.frame': 3 obs. of 6 variables:
## $ D: int 1 2 3
## $ E: int 4 5 6
## $ F: int 7 8 9
## $ D: int 1 2 3
## $ E: int 4 5 6
## $ F: int 7 8 9
## tre_per_tre : 'data.frame': 3 obs. of 3 variables:
## $ D: int 1 2 3
## $ E: int 4 5 6
## $ F: int 7 8 9
## tre_per_tre_logica : logi [1:3, 1:3] TRUE TRUE FALSE TRUE TRUE FALSE ...
## tre_selezioni : logi [1:3] TRUE FALSE TRUEPer fare un po’ di pulizia è possibile usare la funzione rm().
rm() prende come argomento i nomi degli oggetti da rimuovere come nomi (senza virgolette), come vettori di caratteri o come lista (per esempio generata da ls()). Prova nella console questi comandi:
copia_Arthritis <- Arthritis
rm(Arthritis)
# salvo l'abiente come immagine (vedi capitolo 5)
save.image(file = "lambiente.Rdata")
# gli oggetti che iniziano con la A
rm(ls(pattern = "^A"))
# tutti gli oggetti
rm(list = ls())
# ricarico tutto
load(file = "lambiente.Rdata")4.13 Altre risorse.
Riporto, per comodità (tua), risorse già citate in altri capitoli.
4.13.1 Risorse in italiano.
Documenti e pagine web.
Questa wiki di Agnese Vardanega mi pare la cosa migliore.
4.13.2 Risorse in inglese.
Documenti e pagine web.
Riporto qui alcuni libri disponibili online nei quali potrai trovare capitoli rilevanti per il contenuto di questo capitolo:
Libri: provate questi (il secondo è per utenti avanzati)
R for data science: libro assolutamente fondamentale per introdurvi all’analisi dei dati (non necessariamente alla statistica) con R; disponibile on line gratuitamente ma anche come formato cartaceo e epub. Ne esiste anche una traduzione italiana, disponibile qui
Advanced R probabilmente la bibbia della programmazione con R, solo per avanzati
Hands-on programming with R: anche questo un buon libro sulla programmazione in R, più semplice del precedente.
R programming for data science: anche questo bel libro dedicato alla programmazione, corredato da video efficaci
documenti e siti web:
Quick-R: guida di riferimento rapido a strutture di dati e funzione di base
Cookbook for R: un pochino disordinato, ma utile
che c’è di male, è quello che faccio io, fra le varie cose↩︎
la terminologia utilizzata per descrivere i caratteri soggetti a variabilità varia molto da un ambito disciplinare all’altro. Se volete utilizzare la terminologia inglese e leggere un’interessante discussione sulle variabili e sulla variabilità in biologia leggete qui↩︎
si tratta di misure in centimetri, riportate con una sola cifra significativa dopo il separatore decimale; la scelta potrebbe essere dovuta sia a limitazioni dello strumento usato per la misura (per esempio un calibro a nonio, che può apprezzare, al meglio, differenze di 0,05 cm) sia a considerazioni di ripetibilità della singola misura. E’ da notare che per queste misure non sono, ovviamente, possibili valori negativi.↩︎
nelle variabili per scala di rapporti la posizione dello 0 non è arbitraria e quindi ha senso usare confronti basati sia sulle differenze che sui rapporti: 4 cm è il doppio di 2 cm, e così via; di conseguenza è possibile per esempio usare statistiche basate sui rapporti, come il coefficiente di variazione↩︎
questo non è sempre vero; in molti casi, specialmente nella statistica multivariata le tabelle, quando composte da un unico tipo di dati, possono essere trasposte, scambiando righe con colonne↩︎
è importante il corretto uso di maiuscole e minuscole, come vedrai dopo R è un linguaggio “case sensitive”.
Arthritise ‘arthritis’ non sono la stessa cosa…↩︎e probabilmente con un sistema chiamato a doppio cieco, in cui né chi rileva lo stato del paziente né il paziente sanno a che gruppo il paziente appartiene↩︎
in R, un fattore ordinato; i tre livelli (
None, nessun miglioramento;Some: qualche miglioramento;Marked: evidenti miglioramenti) hanno un ordine. Tuttavia non è possibile usare una scala continua, ma solo una scala per ranghi:Markedè certamente “migliore” diSomeetc.↩︎questa notazione indica che mpg appartiene alla libreria ggplot2, che a sua volta appartiene al gruppo di pacchetti del tidyverse↩︎
mentre una tabella è un oggetto matrix-like, simile ad una matrice, un array può avere 3 o più dimensioni↩︎
in un database relazionale diverse tabelle sono collegate da “relazioni”: per esempio la tabella flights è collegata alla tabella airlines tramite l’abbreviazione a due lettere carrier, che compare in entrambe le tabelle: è una cosiddetta variablile chiava (key variable), che può essere usata per unire i dati delle due tabelle in un’unica tabella.↩︎
incidentalmente la temperatura, in questo caso in gradi °F, è un esempio di variabile continua per scala ad intervallo, nella quale la posizione dello 0 è arbitraria ed è possibile fare confronti per sottrazione ma non per rapporti: un oggetto a 212°F non è due volte più caldo di un oggetto a 106°F. Diverso è il caso della scala °K, che è una variabile continua per scala di rapporti, perché la posizione dello 0 non è arbitraria.↩︎
ed è, incidentalmente, la ragione per cui R, con le sue potenti capacità di data wrangling, è probabilmente il miglior linguaggio per la data science. Come potrai facilmente constatare in brevissimo tempo, ci sono molti e fantasiosissimi modi di produrre tabelle sostanzialmente inutilizzabili per l’analisi dei dati.↩︎
quelli mancanti in modo esplicito, vedi dopo↩︎
con un numero di repliche diverso di repliche per ciascun trattamento↩︎
anche se alcune operazioni di riarrangiamento dei dati, come il passagio da tabelle in formato “largo” o “wide” a tabelle in formato “lungo” o “long” potrebbe evidenziare il problema, vedi più avanti in questo libro↩︎
può sembrare banale in una tabella piccola, ma immaginate di avere tabelle di milioni di osservazioni↩︎
prova a leggere questa vignette ↩︎
not a number, può essere generato da operazioni come sqrt(-2)↩︎
se vuoi sapere di più paradigma della programmazione orientata ad oggetti, che è supportata da linguaggi molto popolari come C++, Python e Java, leggi questo articolo su Wikipedia o puoi studiare il libro Advanced R↩︎
che è una parafrasi di “To understand computations in R, two slogans are helpful: Everything that exists is an object. Everything that happens is a function call.” — John Chambers; anche le funzioni sono oggetti!↩︎
in realtà è possibile violare queste limitazioni mettendo i nomi “proibiti” o meglio, non sintattici, fra virgolette singole↩︎
esistono anche i tipi
complexeraw↩︎in realtà
NAha come tipological, provare per credere; per creare specificamente valori mancanti a carattere o numerici occorre usareNA_character_o, per i numerici,NA_real_oNA_integer_↩︎più avanti vedrai che esiste un comando generico,
vector()che permette di produrre un vettore di una data lunghezza e tipo↩︎lo vedrai quando parlerò di importazione di dati: non è sempre ovvio in che modo una colonna di dati verrà importata↩︎
è importante capire che alcune funzioni restituiscono sempre un data frame, e non una matrice e che non sempre le funzioni che richiedono matrici come input accettano data frame assimilabili o trasformabili in matrici: per questo è necessario leggere bene la sezione
valuedell’aiuto di una funzione↩︎se tutti i data frame fossero
tibbleil mondo sarebbe più ordinato,tidy, e semplice; per quanto pigr* ti imbatterai presto nei tanti difettucci deidata frame. Se vuoi saperne di più su alcune proprietà speciali delle tibble, clicca qui ↩︎nota che se il tuo sistema operativo è vecchiotto potresti dover installare R 3.2!↩︎
mandare un data frame di 1.000.000 di righe in stampa in console può essere piuttosto dispersivo↩︎
in realtà sono liste con classi particolari, che ne determinano il modo di stampa↩︎
il pacchetto
lubridatefornisce molte funzioni convenienti e facili da ricordare per questo tipo di oggetti↩︎dei singoli elementi in vettori con una dimensione o liste, delle righe o delle colonne o degli strati in elementi in 2 o più dimensioni↩︎
non funziona con i vettori atomici, come matrici e array↩︎
nota che in RStudio, quando si scrive nella console o in uno script, appariranno suggerimenti man mano che si scrive; per prova a scrivere
Arthritis$: vedrai che apparirà una lista delle variabili del data frame, che si restringerà man mano che si scrivono altri caratteri, o nella quale si può navigare con i trasti freccia e accettare con tab, o invio)↩︎altrimenti restituisce
NULL↩︎in effetti si chiamano “infix functions”; puoi verificare facilmente che
+(1,2) funziona (e domandarti perché ho dovuto usare quel particolare tipo di virgolette intorno al +)!↩︎